Em um post anterior, comentei sobre as possibilidades da utilização de Análise Envoltória de Dados – DEA para a realização de comparações de produtividades combinadas. Hoje vou falar um pouco de mais um ramo da matemática que pode ter aplicabilidades na otimização de um negócio – a teoria dos grafos.
A teoria dos grafos estuda a relação entre indivíduos dentro de uma rede, através de estruturas denominadas grafos. Um grafo nada mais é que um conjunto de pontos (que podem ser indivíduos, instalações, países…) que contenham relações entre si. Por exemplo, em uma rede de pessoas, eu, Fernando, posso ser amigo do Jean e do Paulo, que também são amigos entre si, e o Jean pode ser o único amigo da Bruna. Esse é um exemplo de grafo, que pode ser representado graficamente como mostra a Figura 1.

Figura 1 – Representação de um exemplo de grafo de uma rede de indivíduos
Fonte: ILOS
O grafo também pode ser representado por uma matriz quadrada, chamada de matriz de correspondência, onde o número 0 representa ausência de relação, e o número 1 no caso (podem ser outros, caso haja pesos para as relações) representa a presença de uma ligação.
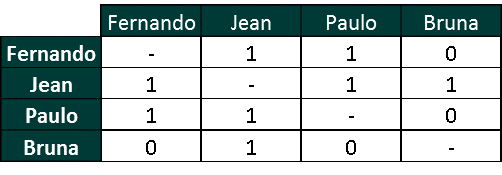
Figura 2 – Representação do mesmo grafo através da Matriz de Correspondência
Fonte: ILOS
Um dos primeiros casos em que se tem registro do uso da teoria dos grafos é no problema das pontes de Königsberg, cidade que possuía quatro ilhas ligadas por sete pontes (como mostra a Figura 3). O matemático Leonhard Euller provou através da teoria dos grafos que era impossível passar uma única vez por todas as sete pontes e voltar à mesma ilha de origem sem repetir pelo menos um dos trajetos.
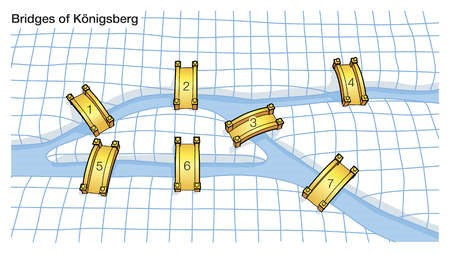
Figura 3 – As Pontes de Königsberg
Fonte: ILOS
Verificar uma rede simples de amigos ou de ilhas ligadas por pontes pode não parecer tão interessante, mas pense que o mesmo tipo de representação pode ser aplicado a redes de centros de distribuição, aeroportos ou portos, redes de fornecimento, de clientes ou até mesmo de pessoas dentro de uma empresa.
A parte mais interessante da teoria dos grafos é poder entender quais são os indivíduos que são mais influentes dentro de uma rede, através de diversas medidas de centralidade. Estas podem aferir quais vértices (o nome técnico dado a cada indivíduo) do grafo são mais influentes, de variadas maneiras. Por exemplo, é possível determinar o indivíduo mais influente baseado no número total de relações (que são chamadas de arestas) que ele possui com outros vértices da rede, que seria a chamada centralidade de grau. É possível também analisar qual é o vértice mais presente nos caminhos mais curtos entre dois vértices quaisquer, através da medida de centralidade de intermediação. Esses são só alguns exemplos de medições que podem ser realizadas para entender a influência de indivíduos dentro de uma rede. Nas referências abaixo, você pode ver mais detalhadamente cada uma delas.
Existem alguns softwares gratuitos que podem gerar relatórios que calculam essas medidas e/ ou representam graficamente uma rede, com múltiplas opções de filtro e exibição. Um deles é o UCINET, que vem acompanhado do Net Draw (que exibe a representação gráfica do grafo) e é bastante simples de utilizar. Basta criar uma matriz de correspondência no próprio programa ou importar uma do Excel, e gerar as análises desejadas.
Com as análises corretas, a teoria dos grafos pode ser muito útil para problemas de roteamento e otimização de redes de forma geral, sendo um conhecimento muito agregador para o profissional da logística.
Referências
<http://www.ime.usp.br/~pf/teoriadosgrafos/texto/TeoriaDosGrafos.pdf>
<http://mathworld.wolfram.com/KoenigsbergBridgeProblem.html>
<http://objdig.ufrj.br/60/teses/coppe_m/LeandroQuintanilhaDeFreitas.pdf>