Diversos pesquisadores concentraram seu trabalho no estudo da aplicação de sofisticadas técnicas de modelagem a um ambiente portuário e aos complexos relacionamentos entre os níveis de custo e serviço que possam eventualmente surgir. Especificamente em relação à operação da ligação navio-ancoradouro (SBL, do inglês ship-berth link), pode-se argumentar que, qualquer que seja o tipo de carga manuseada nos portos, os operadores de navios não apreciam que a fila seja gerenciada por causa do congestionamento do ancoradouro (Dasgupta e Ghosh, 2000). De fato, os operadores de navio que não recebem certas garantias de disponibilidade de ancoradouro podem buscar portos alternativos para manter os altos níveis de produtividade (Luo e Grigalunas, 2003). Como consequência direta, os portos foram forçados a considerar a qualidade do serviço oferecido e também os custos totais de demurrage (sobrestadia).
Se as autoridades portuárias puderem planejar e controlar as operações de SBL em regime diário de curto prazo, dadas as características dos navios e os segmentos de mercado que atendem em médio/longo prazos, elas serão capazes de planejar adequadamente os investimentos futuros na expansão de ancoradouros e também estarão mais bem preparadas para tratar da crescente concorrência (Ho e Ho, 2006). Dentro deste contexto, a simulação de operações portuárias pode ser uma opção para tratar destas questões, na medida em que contribui para avaliar o desempenho do porto e gerar diferentes cenários para ajudar na tomada de decisões (Duinkerken et al., 2006).
O conceito de simulação não é novo. A simulação como ferramenta de pesquisa data dos anos 1960 e foi aplicada a diferentes áreas da pesquisa de logística, tais como o projeto e operação dos sistemas de transporte, o layout e manuseio de materiais de armazéns e a determinação de políticas de ordenação para sistemas de estoque (Casaca, 2005).
Há um crescente número de estudos que tratam do planejamento de SBL (Imai et al., 2001 e 2005). SBL refere-se à interface entre as partes em terra e em água. Tradicionalmente, o problema de planejamento de SBL compreende a atribuição de navios que chegam a posições de atracação, assim como a programação de guindastes de cais, que desempenham um importante papel na gestão das operações portuárias (Meisel e Bierwirth, 2008). Os modelos de simulação têm sido amplamente usados no planejamento e análise do problema de SBL (Dragovic et al., 2005).
Neste trabalho, nos concentramos na análise das estatísticas de espera de navios e nos custos totais de sobre-estadia sob diferentes normas de alocação de ancoradouro e prioridades de fila, através de modelos de simulação desenvolvidos no software Arena. O modelo é suprido com dados provenientes de um estudo de caso confidencial sobre um porto particular brasileiro, no estado de São Paulo. Os resultados são analisados em termos da combinação mais adequada de norma de alocação de ancoradouro e prioridades de fila para um determinado conjunto de níveis críticos de tempos de espera em fila (após o qual são incorridos os custos de sobre-estadia) e diferentes coeficientes de custos de demurrage entre grandes e pequenos navios.
REVISÃO DA LITERATURA
Casaca (2005) apresentou uma estrutura abrangente de operações da indústria portuária, descrevendo em detalhes seus três principais subsistemas: a interface do lado do navio ou área de ancoradouro, o pátio de contêineres e os portões de acesso rodoviário e ferroviário. Sua estrutura deixa claro que as operações portuárias são complexas por natureza e, portanto, exigem sofisticadas técnicas de modelagem, tais como simulação, algoritmos genéricos e programação não-linear para ajudar as autoridades portuárias nos diferentes aspectos da tomada de decisão. A estrutura apresentada por Casaca também é útil para mapear e organizar as pesquisas encontradas na literatura de acordo com seus principais motivadores, a técnica de modelagem adotada, o subsistema estudado e as principais decisões tratadas.
Por exemplo, à medida que a maior parte das empresas de embarque começaram a operar grandes navios de contêineres nos últimos anos, diversos autores usaram a simulação para analisar seu impacto sobre o pátio de contêineres, sob diversas situações. Chang (2005) dividiu um terminal de contêineres em três subsistemas similarmente a Casaca e modelou diferentes padrões de operação que envolvem as operações de atracação, de modo a testar os possíveis cenários de enfileiramento no pátio de contêineres. De forma similar, Tu e Chang (2006) usaram o software de simulação para construir diferentes modelos de operações de atracação e examinaram possíveis cenários no pátio de contêineres. Ambas as pesquisas constataram que as operações da parte do navio poderiam ser consideravelmente responsáveis pelos atrasos no pátio de contêineres.
Em relação aos portões, Parola e Sciomachen (2005) apresentaram um modelo de simulação de evento discreto para analisar como enfrentar o impacto do crescimento no tráfego marítimo sobre a infraestrutura em terra. Mais precisamente, os autores estudaram o impacto do nível de saturação das linhas ferroviárias e sobre o nível de congestionamento dos portões de acesso de caminhões. Por sua vez, Kim et al. (2003) sugeriu um modelo de programação dinâmico para a chegada de caminhões. Diversas regras sequenciais também foram comparadas através de simulação. Os autores constataram que a regra de tempo de processamento mais curto mostrou um nível robusto e elevado de desempenho em diversas situações.
O manuseio de contêineres e sistemas de transporte inter-terminais também podem ser objeto de análise. Por exemplo, Duinkerken et al. (2006) apresentaram uma comparação entre três sistemas de transporte para transporte terrestre de contêineres entre terminais. Ottjes et al. (2006) propôs uma estrutura genérica de modelo de simulação para o projeto e avaliação dos sistemas multiterminais para manuseio de contêineres. Em ambos os estudos, os experimentos realizados deram uma melhor percepção sobre a importância das diferentes características dos sistemas de transporte e sua interação com os equipamentos de manuseio.
Entretanto, independentemente da natureza do subsistema portuário sob análise e da técnica de modelagem empregada, uma coisa fica clara: a competitividade de um porto é especialmente medida em termos de um nível de serviço adequado oferecido às operadoras de navios ou aos usuários (Legato e Mazza, 2001). Assim, uma meta central para as autoridades portuárias é reduzir o tempo de espera de navios, desde a ocasião em que chegam ao porto até o instante de partida, através de um melhor gerenciamento dos recursos atuais, o que certamente exige grande gasto de capital e longo período de retorno (Ho e Ho, 2006). Neste sentido, uma consideração mais atenta da interface do lado do navio, e mais particularmente do SBL, é tida como necessária. Esta ligação não apenas é responsável por uma parte substancial do investimento necessário para construir um porto, mas também pelo tempo total de espera na fila até o início das operações de (des)carga.
A operação de SBL tem sido diversas vezes referida como sistema de planejamento de ancoradouro (Legato e Mazza, 2001), planejamento de alocação de ancoradouro (Nishimura et al., 2001), problema de alocação de ancoradouro (Meisel e Bierwirth, 2008) e operações ancoradouro-guindaste (Canonaco et al., 2008). Em termos gerais, a principal tarefa da operação de SBL é alocar um número limitado de ancoradouros entre navios que chegam. A escolha da atracação de um navio em vez de outro em um ancoradouro específico pode resultar em uma distância muito longa do ponto de localização de seus contêineres no pátio, gerando efeitos cruzados em termos de atrasos, não só nas operações do pátio de contêineres, mas também na fila de atracação (Meisel e Bierwirth, 2008).
Outro recurso comum da operação de SBL é a necessidade de tratar das limitações de recursos e restrições físicas. O número limitado de ancoradouros e guindastes de cais restringe a capacidade de serviço dos portos e terminais, frequentemente levando a um compromisso entre investimentos em ativos fixos e os custos totais de sobre-estadia. Nesses casos, o uso de simulação como uma ferramenta de planejamento tem sido cada vez mais importante para se encontrar um equilíbrio entre as prioridades de fila e a possibilidade de postergar estes investimentos.
Dragovic et al. (2005), que relatou sobre diversos modelos de simulação diferentes em relação às operações portuárias, particularmente examinou o impacto da introdução de prioridade, para certas classes de navios, sobre o desempenho de SBL. Um de seus modelos de simulação indicou que atribuir prioridade a navios menores levaria a uma melhoria nos principais parâmetros operacionais, como o número médio de navios na fila e o tempo médio que um navio passa na fila. Pode-se facilmente perceber o papel crucial que o tempo gasto na fila desempenha na redução do tempo de espera total de navios desde a ocasião em que chegam ao porto até o instante de partida. O caminho para um ambiente portuário ágil deve envolver alguns aspectos fundamentais da gestão de operações (Casaca, 2005), como, por exemplo, em um estudo detalhado sobre as normas de prioridades de fila e alocação de ancoradouro.
Conforme destacado por Asperen et al. (2003), espera-se que as regras de prioridade reduzam os custos de espera de navios de alta prioridade. Em seu estudo, foi considerado um esquema simples com duas classes de prioridade – alta e baixa –, em que os navios grandes tinham alta prioridade, e os pequenos baixa prioridade. Aplicar regras de prioridade reduziu a porcentagem de navios de alta prioridade e aumentou a de navios de baixa prioridade, que têm de aguardar. Entretanto, a questão sobre se os custos totais de sobrestadia são reduzidos aplicando-se regras de prioridade, ou até que ponto isso ocorre, depende de quanto um navio de alta prioridade ocioso é mais caro que um navio de baixa prioridade.
Isso ainda resta para ser testado e, de acordo com Dragovic et al., como o custo é uma medida essencial na escolha das estratégias alternativas ao problema de SBL, são necessárias pesquisas posteriores para incorporar uma análise de custo, de modo a identificar a combinação mais apropriada de normas de alocação de ancoradouro e prioridades de fila em um determinado contexto.
Neste trabalho, consideramos o estudo de caso de simulação em um porto de contêineres particular brasileiro como ponto de partida para tratar destas questões. Como o porto é relativamente pequeno, com apenas dois ancoradouros, foram feitas algumas simplificações aqui no modelo de SBL com a finalidade de aumentar o foco na adequação de diferentes normas de alocação de ancoradouro e prioridades de fila.
Diferentes níveis críticos para tempos de espera em filas e penalidades para sobre-estadia são analisados em uma operação em que a escolha da atracação de um navio em vez de outro em um ancoradouro específico é considerada como não tendo impacto na distância em relação ao ponto de localização de seus contêineres no pátio. Outra simplificação está relacionada ao número de elevadores e guindastes de cais: seu impacto sobre a operação é considerado como integrado dentro dos tempos de processamento médios para cada navio, independentemente do ancoradouro usado. Finalmente, também se considerou que o restante dos recursos do porto, além do escopo da operação de SBL modelada no Arena, não afeta o tempo gasto na fila para cada navio.
OBJETIVOS
Com base na análise da literatura, foram definidas as seguintes questões para este estudo de simulação. A primeira diz respeito à quantificação dos impactos da alocação de ancoradouro e prioridades de fila sobre o tempo que um navio passa na fila. É dada como se segue:
1 – Qual é o impacto de diferentes normas de alocação de ancoradouro e prioridades de fila sobre os tempos de espera para o sistema portuário como um todo e para cada um dos navios que periodicamente visitam o porto?
Neste estudo, foram consideradas quatro normas de alocação de ancoradouros diferentes:
- Ancoradouros dedicados por tipo de navio. Ou seja, dependendo do tamanho do navio, um ancoradouro atende exclusivamente a navios pequenos e outro, a navios grandes;
- Fila única distribui navios para o primeiro ancoradouro disponível. Neste caso, quando todos os ancoradouros atendem a ambos os tipos de navios (pequenos e grandes), os mesmos são mantidos em apenas uma fila antes de serem direcionados para o primeiro ancoradouro disponível;
- Navios alocados ao ancoradouro com o menor tamanho de fila. De acordo com esta norma, os navios entram na fila com o menor tamanho em um determinado momento, implicando assim que todos os ancoradouros atendem a todos os tipos de navios. Diferentemente da última norma, não há fila única que detenha os navios até que um ancoradouro seja disponível;
- Navios alocados ao ancoradouro com menor tempo de fila. Norma similar à última, com exceção do fato de que os navios entram na fila com o menor tempo esperado para começar a atracação em um determinado momento, com base na soma do tempo esperado para o processamento de navios que já estão aguardando na fila.
Em relação às prioridades de fila, foram consideradas oito disciplinas diferentes dentro de cada norma de alocação de ancoradouro (Hansen, 1972; Silberholz et al., 1991). Considera-se que essas disciplinas decidam, no momento em que um ancoradouro fica disponível, qual navio na fila será atendido a seguir. Estas são dadas abaixo:
- Maior tempo de processamento.De acordo com esta prioridade, o navio com maior tempo de processamento, quando um ancoradouro fica disponível, é atendido primeiro. Esta prioridade é o oposto do Menor tempo de processamento;
- Maior número de chegadas de navio por ano.De acordo com esta prioridade, o navio com maior número de visitas programadas por ano é atendido primeiro. Esta prioridade é o oposto do Menor número de chegadas de navio por ano;
- PEPS(Primeiro a entrar, primeiro a sair) e UEPS (Último a entrar, primeiro a sair), duas disciplinas de enfileiramento clássicas e bem conhecidas (vide, por exemplo, Nahmias, 2001);
- Navio de maior tamanho.De acordo com esta prioridade, o navio maior é atendido primeiro quando um ancoradouro está vazio. Esta prioridade é o oposto do Menor tamanho de navio.
As possíveis alternativas para a operação de SBL são ilustradas na Figura 1 através de diferentes fluxogramas. Estes foram modelados no Arena 8.0, uma ferramenta de simulação bem estabelecida para eventos discretos (Chung, 2004). Elas basicamente indicam a mesma sequência de atividades e decisões, diferindo apenas pelos fatores que estão sendo testados. Em termos gerais, o atendimento do navio começa com a sua chegada ao porto. Dependendo do congestionamento e da prioridade atribuída ao navio que chega, ele pode ter que aguardar até que um ancoradouro esteja disponível. Após a atracação, os contêineres são descarregados e/ou carregados no navio. Finalmente, quando o serviço é concluído, o navio deixa o porto.
| (1) Ancoradouros dedicados por tamanho do navio |
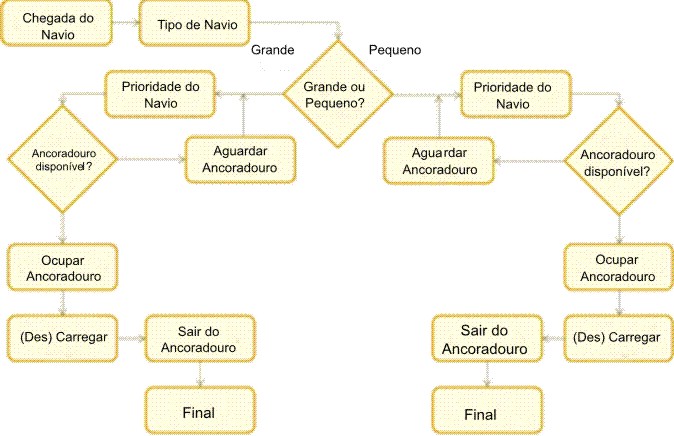 |
| (2) Distribui navios ao primeiro ancoradouro disponível |
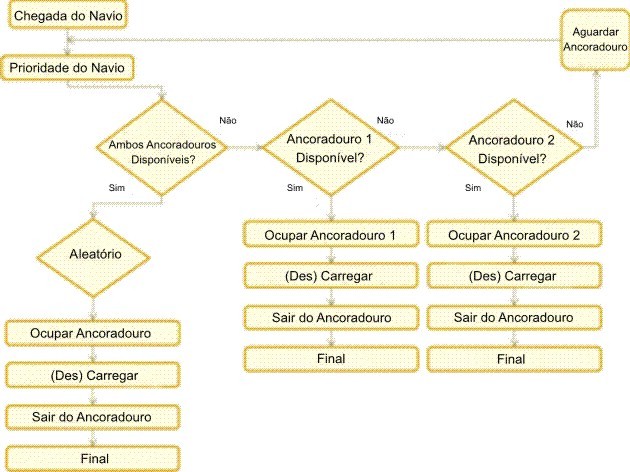 |
| (3/4) Navios alocados a um ancoradouro com menor tamanho ou tempo de fila (Q1 e Q2) |
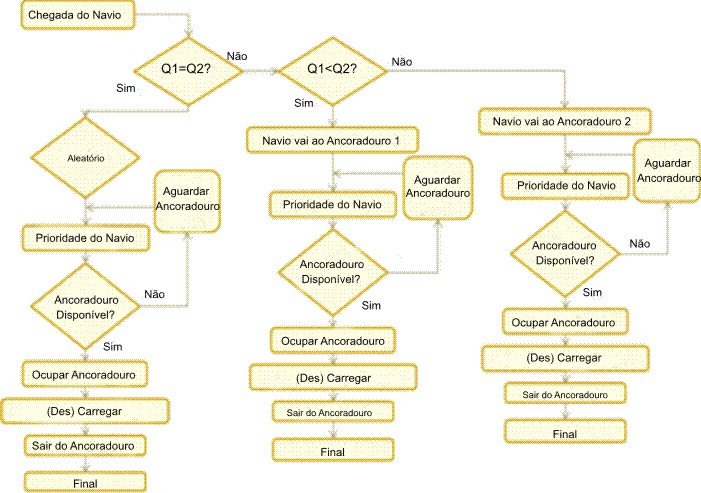 |
| Figura 1: Fluxogramas |
BIBLIOGRAFIA
Asperen, E. V., Dekker, R., Polman, M. e Arons, H. S.. 2003: Allocation of ships in a port simulation. Proceedings of the 15th European Simulation Symposium ISBN: 3-936150-29-X (CD).
Canonaco, P., Legato, P., Mazza, R. M. e Musmanno, R.. 2008: A queuing network model for the management of berth crane operations. Computers & Operations Research 35: 2432-2446.
Casaca, A. C. P.. 2005: Simulation and the lean port environment. Maritime Economics & Logistics 7: 262-280.
Chang, Y. F.. 2005: Analysis of operations at the Kaohsiung port new mega container terminal. The Business Review 4: 123-128.
Chung, C. A.. 2004: Simulation modeling handbook: a practical approach. CRC Press: Boca Raton.
Dasgupta, A. e Ghosh, M.. 2000: Inducing performance in a queue via prices: the case of a riverine port. Management Science 46: 1466-1484.
Dragovic, B., Park, N. K., Radmilovic, Z. e Maras, V.. 2005: Simulation modelling of ship-berth link with priority service. Maritime Economics & Logistics 7: 316-355.
Duinkerken, M. B., Dekker, R., Kurstjens, S. T. G. L., Ottjes, J. A. e Dellaert, N. P.. 2006: Comparing transportation systems for inter-terminal transport at the Maasvlakte container terminals. OR Spectrum 28: 469-493.
Hansen, J. B.. 1972: Optimizing ports through computer simulation: sensitivity analysis of pertinent parameters. Operations Research Quarterly 23: 519-530.
Ho, M. W. e Ho, K. H.. 2006: Risk management in large physical infrastructure investments: the context of seaport infrastructure development and investment. Maritime Economics & Logistics 8: 140-168.
Imai, A., Nishimura, E. e Papadimitrou, S.. 2001: The dynamic berth allocation problem for a container port. Transportation Research Part B 35: 401-417.
Imai, A., Sun, X., Nishimura e Papadimitrou, S.. 2005: Berth allocation in a container port: using a continuous location space approach. Transportation Research part B 39: 199-221.
Kim, K. H., Lee, K. M. e Hwang, H.. 2003: Sequencing delivery and receiving operations for yard cranes in port container terminals. International Journal of Production Economics 84: 283-292.
Legato, P. e Mazza, R. M.. 2001: Berth planning e resources optimization at a container terminal via discrete event simulation. European Journal of Operational Research 133: 537–547.
Luo, M. e Grigalunas, T.. 2003: A spatial-economic multimodal transportation simulation model for US coastal container ports. Maritime Economics & Logistics 5: 158-178.
Meisel, F. e Bierwirth, C.. 2008: Heuristics for the integration of crane productivity in the berth allocation problem. Transportation Research Part E doi: 10.1016/j.tre.2008.03.001.
Nahmias, S.. 2001: Production and operations analysis (Análise de produções e operações). McGraw-Hill: New York.
Nishimura, E., Imai, A. e Papadimitriou, S.. 2001: Berth allocation planning in the public berth system by genetic algorithms. European Journal of Operational Research 131: 282-292.
Ottjes, J. A., Veeke, H. P. M., Duinkerken, M. B., Rijsenbrij, J. C. e Lodewijks, G.. 2006: Simulation of a multiterminal system for container handling. OR Spectrum 28: 447-468.
Parola, F. e Sciomachen, A.. 2005: Intermodal container flows in a port system network: analysis of possible growths via simulation models. International Journal of Production Economics 97: 75-88.
Silberholz, M. B., Golden, B. L. e Baker, E. K.. 1991: Using simulation to study the impact of work rules on productivity at marine container terminals. Computer & Operations Research 18: 433-452.
Tahar, M. R. e Hussain, K.. 2000: Simulation and analysis for the Kelang Container Terminal operations. Logistics Information Management 13: 14–20.
Tu, Y. P. e Chang, Y. F.. 2006: Analyses of operations of ditch container wharf and container yard. The Journal of American Academy of Business 9: 139-146.