A gestão estratégica de estoques vem ganhando importância cada vez maior na gestão da cadeia de suprimentos.
Com o aumento da competição global e a pressão sobre o mercado, as empresas se colocam em busca de vantagens competitivas, tais como customização de serviços e produtos, melhoria no nível de serviço e redução dos custos totais. O desafi o maior é assegurar elevados níveis de serviço ao menor custo.
Pesquisa realizada pelo ILOS1 revela a importância dos custos com estoque para as empresas brasileiras. Dos custos logísticos totais, os estoques constituem uma parcela de 26%, porcentagem menor apenas que os gastos com transportes. A mesma pesquisa revela, ainda, que os custos logísticos representam 11,6% do Produto Interno Bruto nacional, dos quais 3,5% são relativos aos estoques.
Os estoques aparecem na cadeia de suprimentos sob diversos formatos, tais como insumos, produtos acabados e semiacabados. Também podem estar na forma de peças de manutenção, reparo e operação, conhecidas como MRO (Maintenance, Repair and Operation).
Além destes, existem diversos outros fatores que contribuem para uma preocupação crescente com a política de gestão de estoques. Wanke (2003) cita alguns deles:
• A proliferação de SKUs, que torna mais complexa a determinação dos tamanhos dos lotes, pontos de pedido e estoques de segurança;
• O elevado custo de oportunidade do capital – ao manter estoques, a empresa imobiliza parte do seu capital de giro, que poderia ser aplicada no mercado financeiro;
• A redução do Capital Circulante Líquido (diferença entre ativo circulante e passivo circulante), indicador financeiro importante para empresas que desejam maximizar seu valor de mercado.
Considerando todos esses fatores, as principais decisões a serem tomadas no gerenciamento de estoques são: quanto pedir, quando pedir, quanto manter em estoque de segurança, onde localizar os estoques e como controlar o sistema. A estruturação dessas decisões por parte das empresas pode ser em muito auxiliada usando um mapa de estoque.
Devido à extensão do assunto, o presente artigo será dividido em duas partes. Na primeira, será abordado o conceito de mapa de estoque, bem como formas de se classifi car a demanda, utilizando-se esse conceito. Na segunda parte, serão analisadas três ferramentas desenvolvidas para auxiliar o controle dos estoques. Esta terá ainda um estudo de caso, que vai abordar as políticas de gestão de estoques para uma empresa fabricante de equipamentos para o setor agrícola.
MAPAS DE ESTOQUE
No contexto da gestão de estoques, uma das principais difi culdades está em gerir peças de reposição. Essas peças são fundamentais no suporte às operações de manutenção e na proteção contra falhas nos equipamentos (Silva, 2009). As maiores difi culdades na administração desses itens são seus elevados custos de aquisição, longos tempos de resposta de fornecimento (lead-time), além dos baixíssimos giros (Wanke, 2003).
Grandes companhias chegam a manter mais de 500 mil itens diferentes em estoque (Silver, Pyke e Peterson, 1998), aumentando a complexidade da gestão. A elaboração de um modelo de gestão de estoques requer foco nos itens mais rentáveis para as empresas. Através da metodologia da Análise de Pareto, faz-se a classifi cação ABC dos produtos.
Em geral, 20% dos itens são responsáveis por 80% da lucratividade, justifi cando uma política de controle mais sofi sticada apenas para esses itens.
Além da classifi cação ABC, os itens do estoque são classifi cados de acordo com o comportamento de sua demanda:
alto ou baixo giro, regular, errático, entre outros. Essa classifi cação pode ser feita a partir de fronteiras estabelecidas para diversas variáveis, tais como o consumo histórico médio e as variabilidades no tamanho da demanda, no tempo médio entre demandas e no lead-time. Ao estabelecer essas fronteiras, criam-se mapas conceituais, que denominaremos mapas de estoque.
A construção de um mapa de estoque é fundamental para as empresas, uma vez que, a partir da classifi cação das demandas, pode-se estabelecer a política de controle de estoque adequada a cada item. Na medida em que se diferenciam as demandas, é possível identifi car a distribuição de probabilidade à qual a demanda é aderente. Na literatura são encontradas diferentes formas de se classifi car esses itens.
As peças de reposição podem ser segmentadas, por exemplo, de acordo com o consumo histórico médio:
• Peças de consumo em massa: Consumo superior a 300 unidades por ano.
• Peças de baixo giro: Consumo entre uma e 300 unidades anuais (média de aproximadamente uma unidade diária).
• Peças de baixíssimo giro: Consumo inferior a uma peça por ano.
As peças de consumo em massa
As peças de consumo em massa são as que apresentam menor complexidade para seu controle. Por apresentarem demanda de alto giro e mais regular, torna-se mais fácil realizar previsões. São aderentes à Distribuição de Probabilidade Normal.
Essa distribuição, também conhecida como Distribuição Gaussiana, tem um papel fundamental na estatística.
Casella e Berger (2002) apresentam razões para isso: (1) A distribuição normal e distribuições associadas a ela são tratáveis analiticamente. (2) A distribuição normal tem uma forma de sino familiar, cuja simetria é uma escolha para muitas populações. (3) O Teorema do Limite Central, que sob condições brandas mostra que a distribuição normal pode ser usada para aproximar grande variedade de distribuições em grandes amostras.
A distribuição tem dois parâmetros μ e σ2, onde:
E(X) = μ e Var(X) = σ2
As peças de baixo giro
Uma das dificuldades na gestão de peças de reposição de baixo giro está na impossibilidade de a demanda aderir à curva de distribuição normal, como acontece com as peças de consumo em massa. Para superar esta questão, muitos autores assumem que a demanda é aderente à distribuição de Poisson.
A Distribuição de Poisson é uma distribuição discreta, que nos permite calcular a probabilidade de ocorrência de determinado evento baseado em sua média histórica.
A probabilidade da distribuição de Poisson pode ser dada por:
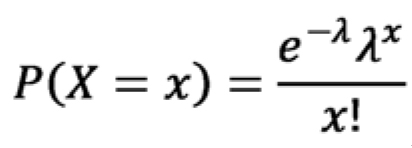 |
onde:
P(X=x) = Probabilidade da demanda de peças ser igual a x unidades;
λ = Taxa de consumo médio por unidade de tempo.
As principais propriedades da distribuição são: E(X) = λ
e Var (X) = λ
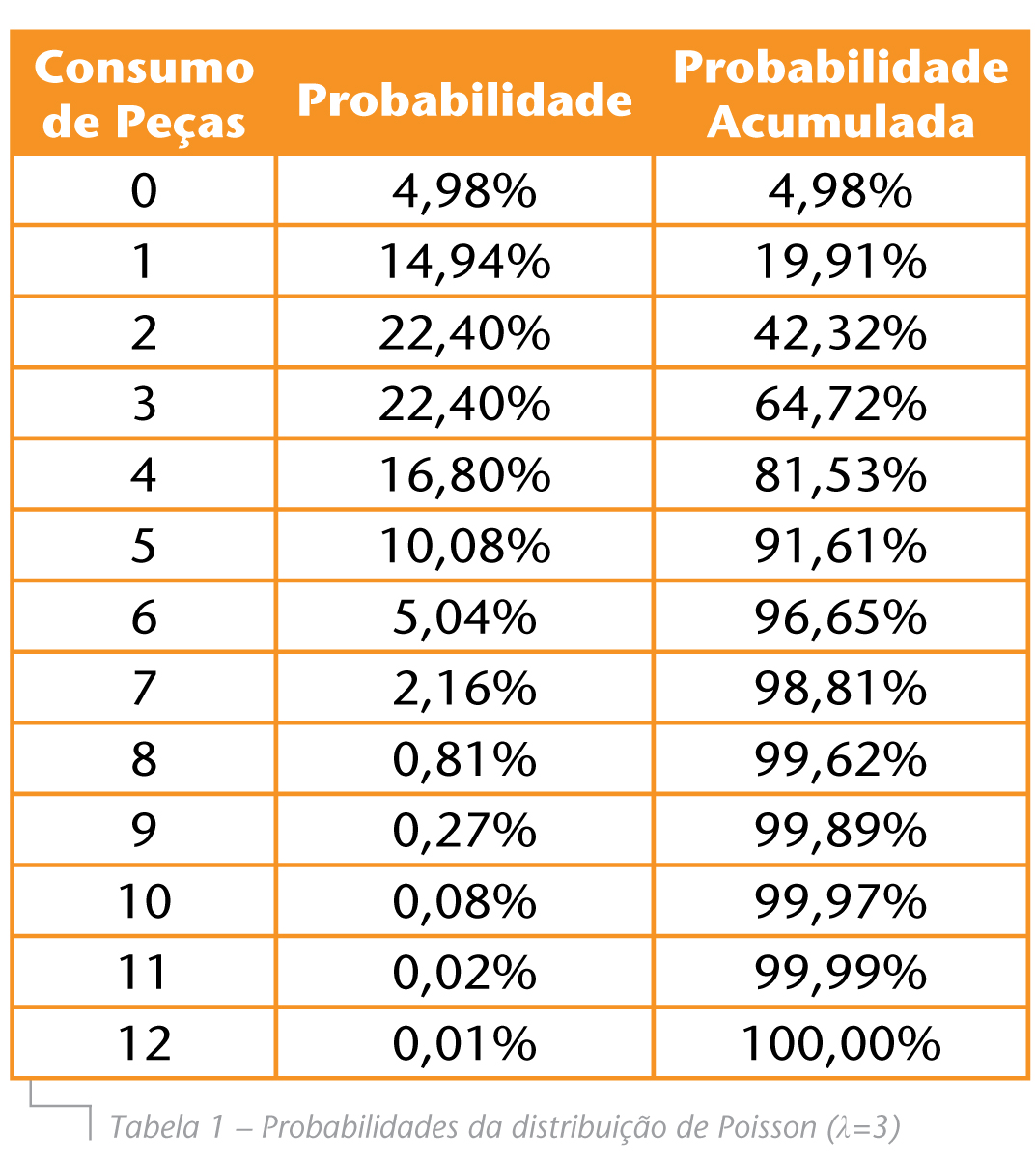
A Tabela 1 ilustra o exemplo de uma peça de reposição com taxa de consumo médio (λ) de três unidades por ano. Foram calculadas as probabilidades individuais e acumuladas de ocorrência de demanda, no horizonte de um ano.
A probabilidade de não haver consumo de peças de reposição é de 4,98%. Por sua vez, a probabilidade de a demanda ser de pelo menos uma peça é de 95,02%. A probabilidade de não haver falta caso o estoque seja igual ao consumo histórico é de 64,72%. Com a manutenção de cinco peças em estoque, a probabilidade de não haver falta é de 91,61%.
O controle de estoques pode ser baseado no tempo de resposta do fornecedor ou ciclo de ressuprimento – intervalo entre a colocação do pedido e o recebimento do mesmo.
Nesse intervalo, a probabilidade de falta de estoques da empresa é maior, já que podem ocorrer imprevistos no ressuprimento. Por isso, é fundamental calcular o ponto de pedido de forma adequada. Este pode ser encontrado através da equação:
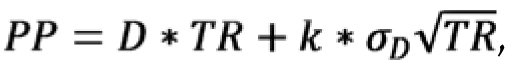 |
onde:
D = Demanda por unidade de tempo;
TR = Tempo de resposta do ciclo de ressuprimento, em unidades de tempo;
k = Fator de segurança;
σD = Desvio-padrão da demanda por unidade de tempo.
Esta fórmula pode ser adaptada para demandas aderentes
à distribuição de Poisson, uma vez que a demanda por unidade de tempo é igual ao parâmetro λ e σD= 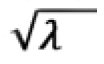 |
Dessa forma, o ponto de pedido pode ser calculado conforme ilustrado:
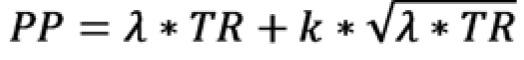 |
Wanke (ANOX) descreve um sistema de apoio à decisão baseado na probabilidade de não haver ruptura de estoque durante o período de ressuprimento. Suponha que uma determinada peça de reposição tenha taxa de consumo (λ) de três peças anuais, o lead-time seja de quatro meses e a probabilidade desejada de não haver falta seja igual a 95%. As probabilidades de não ocorrer falta são mostradas na Tabela 2.
Distribuição Gama
O uso da distribuição Poisson é restrito às situações em que:
0,9 E(X) ≤ V(X) ≤ 1,1E(X)
Se esta restrição não for atendida e o período com demanda nula for superior a 30% do total, alguns autores sugerem o uso da distribuição Gama. Bagchi et al, citado por Yeh, Chang e Chang (1997), consideram que a quantidade pedida em uma demanda (A), o intervalo de tempo entre ocorrências da demanda (T) e o lead-time de ressuprimento (Z) são aderentes à distribuição Gama, com parâmetros (μ,σ), (α,β) e (γ,δ), respectivamente. Assim como na Poisson, pode-se calcular a probabilidade de haver ruptura no estoque durante o lead-time (Os) através da equação:
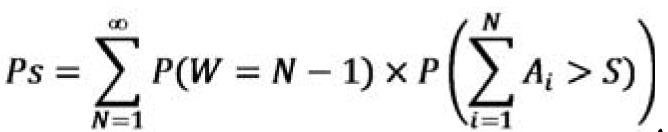 |
onde:
Ps = Probabilidade de haver ruptura durante o leadtime (Z);
Ls = Nível de Serviço (1- Ps);
Ti = Intervalo de tempo entre duas ocorrências de demanda
– parâmetros (α,β);
Ai = Quantidade pedida em uma demanda – parâmetros (μ,σ);
Z = Lead -time de Ressuprimento – parâmetros (γ,δ);
W = Número de ocorrências de demanda no lead-time (Z);
S = Quantidade de estoque remanescente.
As peças de baixíssimo giro
O controle de estoques das peças de baixíssimo giro deve ser baseado na análise dos custos totais, decidindo se é mais apropriado manter uma unidade em estoque ou não mantê-la, disparando a reposição contra pedido (Wanke, 2003).
Sejam as variáveis:
CTR = Custo total associado à colocação de um pedido de suprimento (R$);
Caq = Custo unitário de aquisição da peça (R$);
LT = Lead time de resposta do pedido (meses);
λ = Taxa de consumo histórico por ano (peça/ano);
T = Taxa anual de oportunidade do capital (% ao ano);
Cip = Custo de Indisponibilidade e Penalidade, expresso como um valor absoluto incorrido toda vez que há solicitação da peça de reposição e a mesma não se encontra em estoque (R$).
O custo de não manter o item em estoque é dado pelo cálculo que pode ser visto:
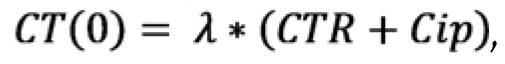 |
E o custo de manter uma peça em estoqueé dado por:
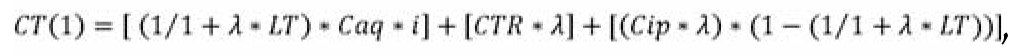 |
A tomada de decisão a partir deste cálculo torna-se mais simples:
se CT(0) > CT(1), o item deve ser mantido em estoque.
Caso CT(1) > CT(0), a peça de reposição não deve ser estocada.
OUTRAS FORMAS DE CLASSIFICAÇÃO DA DEMANDA
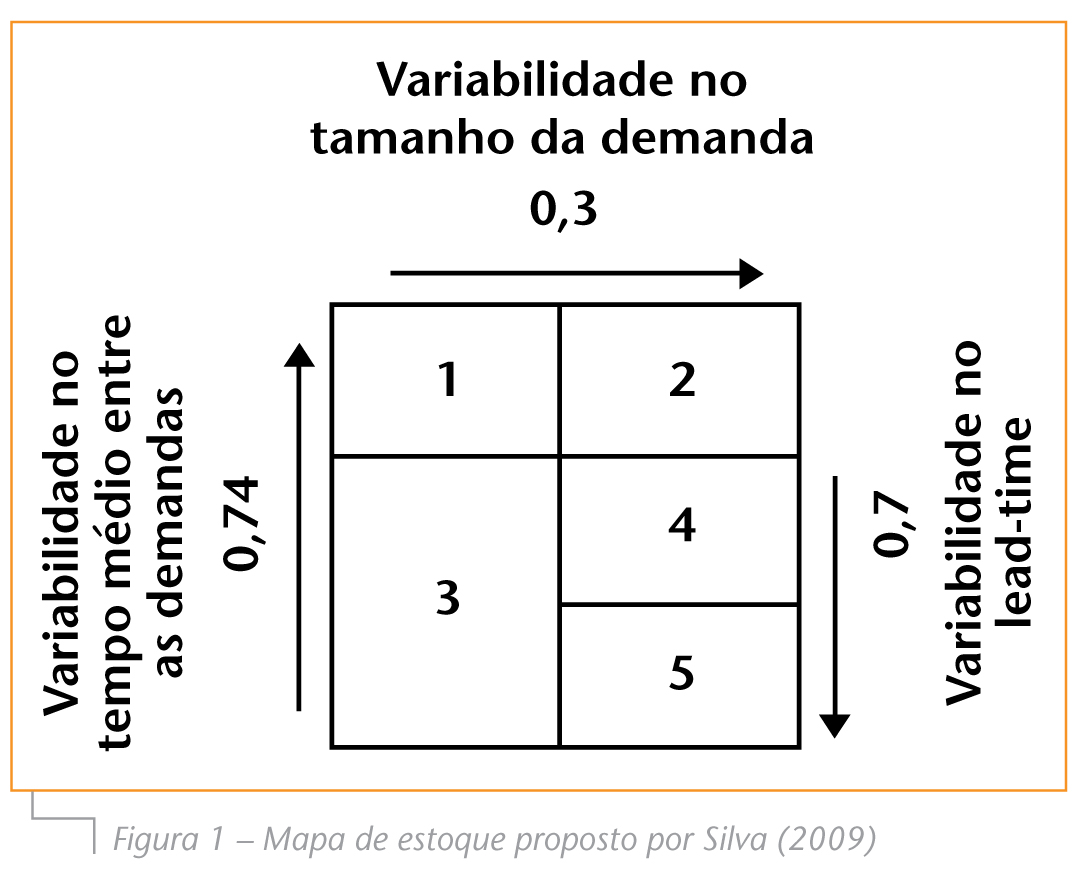
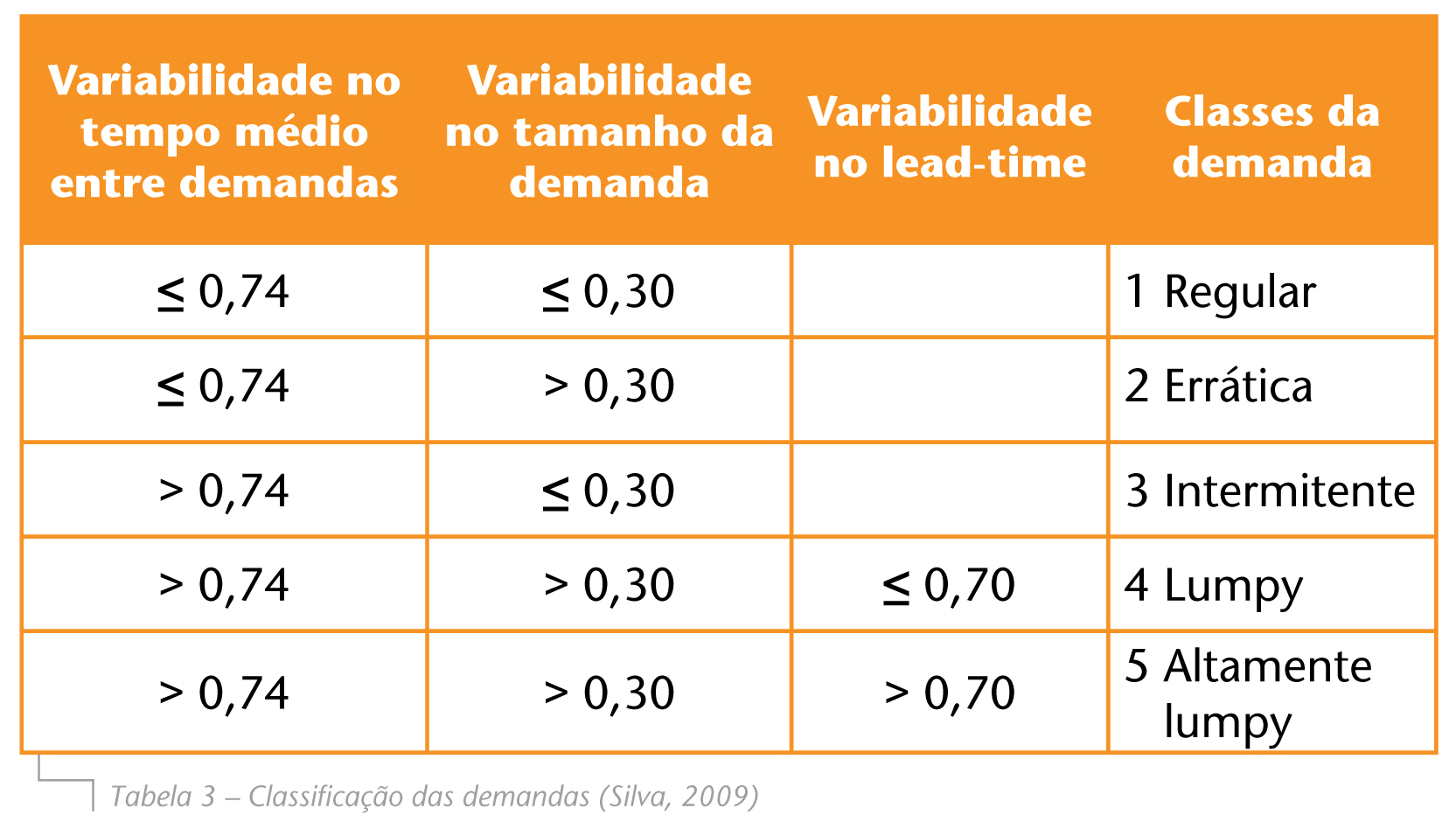
Podemos classifi car a demanda de outras formas, além da já descrita. Silva (2009) usa em sua dissertação uma classifi cação baseada na variabilidade do tempo médio entre as demandas, do tamanho da demanda e do leadtime.
Outras classifi cações surgem, principalmente, da necessidade de classifi car os itens de baixo giro cujo comportamento da demanda é errático – alta variabilidade no tamanho da demanda – e intermitente – alta variabilidade no tempo médio entre demandas. Classifi ca-se uma demanda como “lumpy” quando esta apresenta os padrões errático e intermitente.
A classifi cação feita pelo autor é baseada nos modelos propostos por Eaves e Kingman (2004) – variabilidade dos componentes da demanda durante o lead-time – e por Silver, Pyke e Peterson (1998) – valor esperado da demanda.
Os valores das fronteiras foram obtidos experimentalmente, diferenciando itens de baixo giro (slow-moving) ou alto giro (fast-moving). Essa classificação é mostrada na Tabela 3 e seu respectivo mapa de estoque na Figura 1.
Silva (2009) desenvolveu em seu estudo um modelo para controle de estoques de peças de reposição baseado nessa classifi cação. O controle é feito com base no cálculo dos custos totais de estoque, do fi ll rate e do nível de serviço.
Conclusão
A gestão de estoques cresce em importância na logística das empresas brasileiras. Juntando-se a ela desenvolve se também a preocupação com a redução dos custos de estoque, seja pelo elevado custo de oportunidade do capital imobilizado em estoque ou pela redução do capital circulante líquido.
Entretanto, encontrar uma política de gerenciamento é uma tarefa delicada para as empresas, mas que pode ser simplificada pelo uso de mapas de estoque.
Na literatura existem alguns mapas sugeridos. No entanto, a elaboração de novos mapas ou estabelecimento de outras fronteiras consiste em uma grande oportunidade de desenvolvimento para as empresas, visto que estarão adequando alguns padrões já estudados às necessidades reais. Na segunda parte deste artigo serão abordadas ferramentas construídas com base nos conceitos de mapa de estoque apresentados, além da apresentação de um estudo de caso.
Bibliografia
CASELLA, G.; BERGER, R. L. Statistical Inference. 2nd ed.
Pacifi c Grove. Duxbury, 2002. 660p.
DA SILVA, G. L. C. Modelo de Estoque para Peças de Reposição Sujeitas à Demanda Intermitente e Lead-Time Estocástico.
2009. 75 f. Dissertação (Mestrado em Engenharia de Produção) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte. 2009.
SILVER, E. A.; PYKR, D. F.; PETERSON, R. Inventory Management and Production Planning and Scheduling. 3rd ed.
Jonh Wiley & Sons, 1998. 754p.
WANKE, P. Gestão de Estoques na Cadeia de Suprimentos.
São Paulo. Editora Atlas, 2003.176p.
WARD, J. B. Determining Reorder Points When Demand is Lumpy. Management Science, v. 24, nº.6, pp. 623-632, 1978.
WANKE, P. Gestão de Peças de Reposição de Baixíssimo Giro.
2002. Disponível em: https://ilos.com.br/site/index.
php?option=com_content&task=view&id=1103&Itemid=74 WANKE, P. Gestão de Peças de Reposição de Baixo Giro.
2003. Disponível em: https://ilos.com.br/site/index.
php?option=com_content&task=view&id=767&Itemid=74 YEH, Q. J.; CHANG, T. P.; CHANG, H. C. An Inventory Control Model With Gamma Distribution. Microelectron.
Reliab., v. 37, n. 8, p. 1197-1201, 1997.
1 – Pesquisa do Instituto ILOS – Custos Logísticos no Brasil