Praticamente todos os processos logísticos estão sujeitos a algum tipo de sazonalidade. A humanidade e seus grupos sociais, desde tempos remotos, sempre tiveram suas atividades controladas por algum tipo de evento periódico: inverno e verão, meses do ano, período semanal e mesmo ao longo das horas do dia.
Esta variação rítmica de atividade tem inúmeras implicações, dentre elas um forte impacto nas operações logísticas. A demanda por produtos e serviços é geralmente influenciada por componentes sazonais que devem ser levados em conta para uma utilização mais eficiente dos recursos e oportunidades disponíveis. Neste texto, após discutirmos o conceito técnico de sazonalidade, apresentaremos algumas formas mais simples de como mensurá-la. O uso dos chamados índices sazonais vai além do simples processo de previsão de demanda, sendo também utilizado no acompanhamento de resultados, após descontar o efeito sazonal. Softwares de previsão podem nos auxiliar nesta tarefa. No entanto, deveremos procurar manter sempre um controle do processo de previsão, evitando que este seja visto como o resultado de caixa preta em que os valores são fornecidos sem que o usuário saiba como foram obtidos. Por fim, vale a pena avaliar em que situações uma maior complexidade do processo de determinação dos índices sazonais seria justificável, em lugar do uso de métodos mais simples e também de mais fácil compreensão.
CONCEITO DE SAZONALIDADE
Ao analisarmos uma série de dados de venda de um produto ou serviço, quase sempre observamos um movimento periódico desta série ao longo do tempo. Este movimento periódico, muitas vezes associado aos meses do ano, caracteriza o que denominamos efeito ou componente sazonal. Exemplos práticos não faltam deste tipo de situação: venda de bebidas e alimentos, consumo de combustíveis e energia elétrica, venda de aparelhos eletrodomésticos, ocupação de hotéis, tráfego aéreo, atendimento médico hospitalar, e o mais marcante, as vendas de final de ano.
De fato, em nosso varejo, o mês de dezembro é o mais forte do ano, com vendas usualmente superiores à média dos demais meses do ano em 50% ou mais. Esta flutuação de demanda na ponta do processo (compra pelo consumidor final) gera uma onda que se propaga ao longo de toda a cadeia logística, com as devidas defasagens de tempo. Por exemplo, para que o produto esteja disponível para venda na época natalina, ele deverá ter sido produzido e entregue à loja com a devida antecedência; por sua vez, o seu pedido deverá ter sido preparado mais cedo ainda, assim como todos os insumos da cadeia produtiva/logística deverão ter sido adequadamente previstos.
Do ponto de vista da produção e logística, o mundo ideal seria aquele em que a produção e demanda por um produto ou serviço fosse a mais estável possível, exigindo assim um mínimo de intervenção no processo. Mas, felizmente ou infelizmente, o mundo nunca é como gostaríamos que fosse!
Assim no nosso dia a dia, temos que lidar com não só com as incertezas típicas de um ambiente econômico de natureza aleatória, como também temos que saber levar em conta a sazonalidade em nossos planos e ações. A primeira questão reside em como medir a sazonalidade, melhor ilustrada através de um exemplo.
ÍNDICES SAZONAIS
O primeiro passo na análise de uma série de vendas, antes mesmo de identificar o seu eventual padrão sazonal, consiste em identificar o seu comportamento geral. Assim, vamos considerar o caso de um produto, cuja série de vendas passadas, em unidades/trimestre, é apresentada na tabela 1:
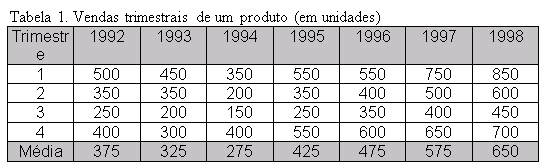 |
Antes de utilizarmos uma técnica quantitativa no estudo de uma série de vendas como esta, deveremos representá-la num gráfico para que possamos identificar seus componentes. Embora outros componentes estejam normalmente presentes numa série de vendas, como o nível e tendência das vendas , nossa preocupação atual reside no componente sazonal. No caso, já se sabia da existência de uma acentuada sazonalidade nas vendas do produto, fato este confirmado pelo Gráfico 1:
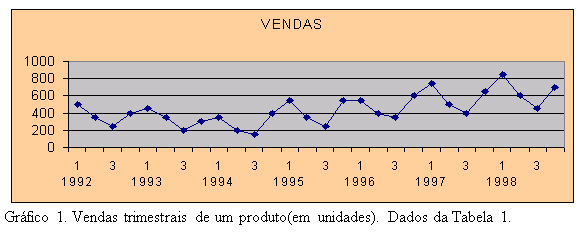 |
Observando este gráfico notamos um movimento regular de oscilação das vendas ao longo do ano, sempre com um pico no primeiro trimestre e um valor baixo no terceiro trimestre. Ora, esta situação, típica de muitos produtos e serviços, leva necessariamente a inúmeros desafios logísticos, tais como o fornecimento de matéria prima que também pode ter uma oferta sazonal, a definição de uma política de armazenagem/produção adequada aos custos envolvidos e às características da situação, uma estratégia de distribuição envolvendo operadores logísticos, distribuidores e clientes e até mesmo uma política de preços. Para que toda esta preparação seja possível, torna-se necessária uma forma de mensuração da sazonalidade, o que é feito através dos chamados índices sazonais.
Em princípio, há duas maneiras de se representar um efeito sazonal:
- Através de um componente aditivo
- Através de um componente multiplicativo
O componente aditivo, como seu nome indica, tem como princípio a soma (adição) de parcelas associadas a cada período sazonal, trimestre no caso. Já o componente multiplicativo é caracterizado pelo uso de um fator multiplicativo para cada período, em geral sob a forma de um percentual. Discutiremos, a seguir, cada uma destas representações, apresentando também possíveis formas de cálculo.
COMPONENTE ADITIVO
O componente aditivo (relativo à operação de soma ou adição) é representado através de um valor fixo para cada trimestre que é somado (ou subtraído) ao valor base das vendas de um determinado período. Assim, por exemplo, as vendas do primeiro trimestre de um ano poderiam ser vistas como a venda média do ano mais, digamos, 129 unidades, enquanto que as vendas do terceiro trimestre – mais baixas- poderiam ser vistas como as vendas médias do ano menos 150 unidades. Da mesma maneira, teríamos um valor a ser aplicado para os demais trimestres do ano. Com base nesta formulação, iremos considerar como uma aproximação que o efeito do trimestre é sempre o mesmo para cada um dos trimestres de cada ano. Assim, o aumento de vendas do primeiro trimestre é, em média, 129 unidades, qualquer que seja o ano considerado, enquanto que as vendas do terceiro trimestre são sempre 150 unidades abaixo da média trimestral. Se isto é uma boa descrição das vendas reais, já é outra estória, mas de qualquer forma já temos um bom começo!
Como então poderíamos calcular este efeito sazonal aditivo?
Não existe uma única forma de fazê-lo, mas uma regra a ser seguida é que a soma dos efeitos sazonais ao longo do ano seja neutra, no caso igual a zero. Tendo esta regra como base, uma forma simples de calcularmos os índices sazonais de cada trimestre (sem nos preocuparmos com a tendência da série) seria através do cálculo das médias de aumento/redução das vendas para cada trimestre do ano, conforme exemplificado na tabela 2:
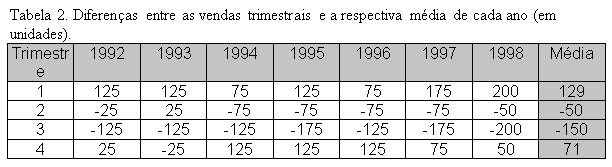 |
Nesta tabela, definida pelas diferenças entre os valores de venda a cada trimestre e a média das vendas do respectivo ano, a soma dos valores de cada coluna, referentes a um mesmo ano, é zero. Assim, para o primeiro trimestre de 1992, o valor 125 indica que o nível das vendas neste trimestre esteve 125 unidades acima da média do ano, enquanto que o valor de –25 do segundo trimestre nos diz que as vendas deste período foram 25 unidades abaixo da média deste mesmo ano. Agora, ao tomarmos a média dos valores de cada um dos trimestres (média das linhas da tabela), teremos uma boa estimativa do efeito sazonal aditivo de cada trimestre.
Assim, com base nos resultados obtidos e supondo que as vendas estimadas para o próximo ano seriam em média de 700 unidade por trimestre, nossa previsão ajustada para a sazonalidade seria de 829 (700+129) para o primeiro trimestre, 650 (700-50) para o segundo, 550 (700-150) para o terceiro e finalmente 771 (700+71) para o quarto trimestre.
Naturalmente, os números obtidos são apenas previsões, mas já devidamente ajustadas às expectativas do nível esperado das vendas e aos componentes sazonais. Continuando em nossa análise, vamos agora supor que as vendas reais para o primeiro trimestre do próximo ano tenham sido de 850 unidades. Como este valor superou nossas previsões, temos duas possíveis explicações para o fato: ou o nível das vendas aumentou ou a sazonalidade foi mais forte que o previsto. De qualquer forma, esta constatação somente foi possível após termos isolado os dois componentes das vendas: nível e sazonalidade.
Mas, o procedimento apresentado não é a única maneira de calcularmos os índices sazonais aditivos. A teoria estatística das previsões propõe outras opções de cálculo que, em geral, são de elevada complexidade e pouco acrescentam em relação a métodos mais simples como o que aqui vimos. De fato, embora diferentes metodologias forneçam resultados diferentes quando do estudo de uma mesma série de vendas, os valores obtidos com métodos mais sofisticados, quando aplicados a este mesmo caso, não diferem substancialmente dos que obtivemos com este simples cálculo de médias, que além de mais fácil é também mais intuitivo.
Na verdade, a principal crítica em relação ao uso de componentes aditivos não reside no procedimento de cálculo dos índices sazonais, mas na sua aplicabilidade prática. São poucas as situações do mundo real em que um efeito sazonal, como uma parcela que se soma ou subtrai a cada período, é uma descrição adequada do comportamento das vendas. O mais intuitivo e usual consiste em considerar-se a sazonalidade não como um efeito absoluto que se soma ou subtrai das vendas, mas como um efeito multiplicativo e relativo, um percentual que se aplica a cada período específico, seja para incrementar as vendas deste período em relação à média, seja para reduzir as vendas do período em função de uma sazonalidade de baixa. Então em lugar de considerarmos as vendas de um período como sendo de 150 unidades a mais, melhor seria considerá-la, digamos, como 40% acima da média. É esta a idéia dos componentes multiplicativos que discutiremos a seguir.
COMPONENTE MULTIPLICATIVO
Uma alternativa aos efeitos aditivos consiste no uso de componentes multiplicativos. Neste caso, um efeito sazonal multiplicativo neutro corresponderia a um índice sazonal igual a 1 (100%), um índice superior a 1, digamos 1.50 (150%), corresponderia a um período com sazonalidade 50% superior a um mês ou dia médio. A representação da sazonalidade como um efeito multiplicativo é uma melhor forma de traduzir a idéia de que a sazonalidade das vendas seria um efeito proporcional ao nível das vendas o que é a prática comum na maioria das empresas.
Tal como ocorre com o componente aditivo, não há uma única forma de calcularmos os seus valores, mas vale também a regra básica de que a soma dos efeitos sazonais ao longo do ano seja neutra; no caso, por serem efeitos que multiplicam nível médio das vendas, sua média deve ser igual a 1 para que o efeito sazonal ao longo de um ano seja neutralizado. Tendo este princípio como base, podemos calcular os índices sazonais multiplicativos para os mesmos dados anteriormente estudados com o modelo aditivo.
No caso, necessitamos de um valor que sirva de base para o cálculo dos efeitos sazonais de cada trimestre. Uma boa opção (existem outras ainda melhores!) é tomar a relação das vendas de cada trimestre com a respectiva média do ano. A tabela 3 ilustra a aplicação desta idéia à nossa série:
 |
Nesta tabela, definida pela divisão dos valores de venda a cada trimestre pela respectiva média das vendas para o mesmo ano, a média dos valores de cada coluna, referentes a um mesmo ano, é um (100%). Assim, para o primeiro trimestre de 1992, o valor 133 % indica que o nível das vendas neste trimestre esteve 33% acima da média do ano, enquanto que o valor de 93% do segundo trimestre nos diz que as vendas deste período foram 93% da média anual ou seja 7% abaixo desta média. Agora, tal como fizemos no caso anterior relativo aos efeitos aditivos, tomamos a média dos valores de cada um dos trimestres (média das linhas da tabela). Com isso, teremos uma boa estimativa do efeito sazonal multiplicativo de cada trimestre.
Assim, com base nos resultados obtidos e supondo que as vendas estimadas para o próximo ano seriam novamente em média de 700 unidade por trimestre, nossa previsão ajustada para a sazonalidade seria de 903 (700*129%) unidades para o primeiro trimestre, 623 (700*89%) para o segundo, 455 (700*65%) para o terceiro e finalmente 819 (700*117%) para o quarto trimestre. Em comparação com os valores ajustados no caso aditivo, observamos que nossas previsões foram agora mais carregadas tanto para os trimestres mais fortes (primeiro de quarto) como para os mais fracos (segundo e terceiro); isto se deve ao fato dos cálculos serem feitos com base no nível estimado de vendas para o próximo ano que, neste caso, é um valor acima da média passada por serem as vendas crescentes ao longo do tempo. A tabela 4 resume esta comparação:
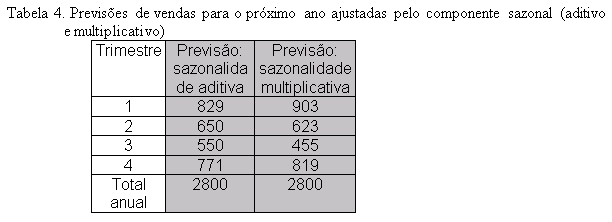 |
Novamente aqui, poderemos avaliar o resultado das vendas futuras em relação ao que esperávamos. Assim uma venda de 850 unidades no próximo trimestre seria um bom resultado ou não? Neste caso, ao contrário do modelo aditivo, a resposta seria não, já que esperávamos uma venda de 903 unidades! Naturalmente, como vivemos em um mundo de incertezas, um resultado como este, apesar de abaixo das expectativas, seria absolutamente normal em função dos elementos aleatórios presentes no ambiente de negócios.
O uso de componentes multiplicativos tem ainda uma vantagem adicional em relação aos componentes aditivos pois permitem uma melhor comparação de sazonalidades entre diferentes produtos, diferentes setores de atividade ou mesmo diferentes estabelecimentos. Esta comparação só seria possível com a adoção de índices sazonais padronizados (com média unitária) ao longo do ano, caso contrário não teríamos uma base comum de referência.
Finalmente, temos novamente outras opções para o cálculo de índices sazonais multiplicativos como por exemplo os métodos conhecidos como decomposição clássica ou o amortecimento exponencial de Holt Winters. Embora estes métodos sejam mais sofisticados e portanto forneçam resultados mais precisos, sua aplicação a este nosso exemplo leva a resultados muito próximos daqueles a que chegamos com um simples cálculo de médias. E esta é uma constatação empírica que os autores de trabalhos de previsão de vendas tem chegado: em geral, métodos relativamente simples fornecem resultados quase tão bons como os métodos mais sofisticados, muitas vezes não compensando o preço de uma maior complicação matemática e dificuldade de compreensão.
CONCLUSÃO
Como pudemos constatar, a sazonalidade pode ser facilmente quantificada seja para gerar previsões, seja para compararmos resultados de diferentes períodos ou de diferentes produtos. Com bom senso e o uso correto de conceitos básicos estatísticos como o cálculo de médias, podemos obter valores quase tão bons quanto aqueles fornecidos por sofisticados e caros softwares de previsão e, melhor ainda, fazermos tais cálculos com uma simples planilha eletrônica.
BOX 1
VALE A PENA UTILIZAR MÉTODOS MAIS SOFISTICADOS PARA A DETERMINAÇÃO DE ÍNDICES SAZONAIS?
Embora existam sempre ganhos de precisão com o uso de métodos mais sofisticados, a prática mostra que estes ganhos não são muitas vezes expressivos de modo a justificar uma maior complexidade estatística, requerendo um conhecimento mais aprofundado das técnicas de previsão e também o uso de softwares mais caros e difíceis. É claro que em geral vale a pena utilizarmos métodos mais elaborados do que os aqui apresentados, particularmente no caso em que os erros de previsão têm custo elevado. Este custo elevado pode ser gerado pela perda resultante de uma previsão pessimista abaixo do real, quando muitas vezes teremos que arcar com custos mais elevados para atendermos as vendas ou mesmo pela perda de vendas por falta de capacidade de produção ou atendimento. Mas temos também a perda decorrente de uma previsão otimista acima do real quando teremos que arcar com um excedente de produtos em estoque que, para serem desovados, necessitarão de um substancial desconto nos preços ou mesmo tornar-se-ão obsoletos no caso de produtos altamente perecíveis ou ainda, no caso de serviços; como o transporte, em que nossa capacidade de operação será sub-utilizada com uma consequente ociosidade.
BOX 2
SOFTWARES DE PREVISÕES
Embora haja uma tendência recente de integração de módulos de previsão em sistemas logísticos e de ERP, existem diversos produtos no mercado voltados para o problema das previsões. Estes produtos são classificados em três categorias: automáticos, semi-automáticos e manuais. Os softwares automáticos, como o nome diz, fazem praticamente sozinhos a tarefa de analisar séries e recomendar o método de previsão mais adequado à situação em estudo com base em critérios estatísticos. Embora representem uma boa opção, eles tendem a ser utilizados como caixas pretas em que o usuário tem pouca ou nenhuma possibilidade de intervenção no processo, aceitando ou não os seus resultados. Um dos produtos mais conhecidos desta categoria é o software Forecast Pro (www.forecastpro.com) cuja versão mais completa custa cerca de US$1000,00. O Forecast Pro incorpora um sistema especialista para a seleção do método de previsão mais adequado para cada série analisada.
Os softwares semi-automáticos de previsão são, em princípio, softwares estatísticos como o SPSS, SAS ou econométricos como o EVIEWS. Neste caso, o usuário faz uma seleção prévia dos métodos a serem testados em seu problema , deixando ao computador a escolha dos parâmetros ótimos que minimizam o erro de previsão. A escolha do método mais adequado é feita pelo usuário com base nos resultados dos vários testes. Finalmente, os softwares manuais são aqueles em que o usuário define o método de previsão a ser testado e respectivos parâmetros; o software é utilizado unicamente para avaliar o desempenho do método proposto. Neste caso, há necessidade de um maior conhecimento técnico por parte do usuário, mas em compensação tem-se um maior controle do processo de previsão.
BIBLIOGRAFIA
Para um estudo mais aprofundado da determinação de índices sazonais bem como das técnicas de previsões, indicamos três textos, todo em inglês, porém de fácil leitura e aquisição. Uma sugestão para aquisição destes textos é através das livrarias eletrônicas na Internet, como por exemplo a Amazon (www.amazon.com)
DeLurgio, S.A. Forecasting Principles and Applications. New York, McGraw Hill, 1998.
Hanke, J.E. e Reitsch, A G. Business Forecasting. 6 Ed., Prentice Hall, 1998
Makridakis, S., Wheelwright, S. e Hyndman, R.J. Forecasting: Methods and Applications. 3 Ed., New York, Wiley, 1998.
Mentzer, J. e Bienstock, C. Sales Forecasting Management. Sage, 1998.