Conforme foi apontado em outro artigo nesta mesma revista (edição de agosto/2002), a gestão de estoques de peças de reposição constitui um capitulo a parte da gestão de estoques. Isto por que as peças de reposição apresentam substanciais diferenças com relação aos custos de aquisição (em geral mais altos), aos tempos de resposta (em geral mais longos), ao giro dos estoques (em geral mais baixo) e à distribuição da demanda (definitivamente não aderente à distribuição normal) quando comparadas, por exemplo, aos bens de consumo não duráveis e suas matérias-primas.
Especificamente, a impossibilidade de assumir a distribuição da demanda aderente à curva normal, torna bastante complexa a resposta à seguinte questão: qual deve ser o ponto de pedido ou o estoque de segurança de uma determinada peça de reposição para que a probabilidade da falta seja tão pequena quanto se desejar? Diversos livros de estatística, administração de materiais e logística apresentam, nos seus apêndices, tabelas com as probabilidades da distribuição normal acumulada, que tornariam relativamente “mais simples” a resposta para esta questão. O problema é que não se sabe, de antemão, qual a magnitude do erro no planejamento dos estoques decorrente da suposição da distribuição normal quando a demanda definitivamente não tem este perfil.
Um caminho normalmente utilizado para lidar com tal situação é considerar que o perfil da demanda é aderente a distribuição Poisson. As propriedades desta distribuição a tornam particularmente interessante para o entendimento de como diferentes níveis de estoques de segurança afetariam a probabilidade de falta de produto, especialmente em ambientes de baixo giro, ou seja, consumo anual entre 1 e 300 unidades por ano. Por exemplo:
- a distribuição Poisson é discreta, ou seja, é possível calcular a probabilidade de ocorrência de um determinado nível de consumo com base na sua média histórica. Em outras palavras, seria possível responder a questões do tipo: “dado que o consumo histórico de uma determinada peça de reposição é de 50 unidades por ano, qual é a probabilidade do consumo ser exatamente de 4 peças no próximo mês?”
- a distribuição Poisson pressupõe independência entre eventos, ou seja, o nível de consumo de um mês não é afetado pelo consumo do mês anterior e tampouco afetará o consumo nos meses seguintes.
- na distribuição Poisson a variância é igual ao consumo médio num determinado período.
Este artigo tem por objetivo apresentar a distribuição Poisson, ilustrando não apenas como a mesma pode ser utilizada na gestão de estoques de peças de reposição de baixo giro, mas também como implementa-la na Planilha Excel e analisar os resultados obtidos de modo a ampliar os elementos para tomada de decisão.
EXEMPLOS DE APOIO À TOMADA DE DECISÃO
A formula a seguir apresenta como calcular a probabilidade (px(t)), para um dado período de tempo (t), do consumo de peças de reposição ser igual a x unidades, dado que o consumo médio histórico, para um mesmo horizonte de tempo, é de ? unidades.
A tabela 1 apresenta um exemplo considerando uma peça de reposição com consumo histórico de 2 unidades por ano. Para cada nível de consumo possível de ocorrer nos próximos doze meses, são calculadas as probabilidades individuais e as probabilidades acumuladas.
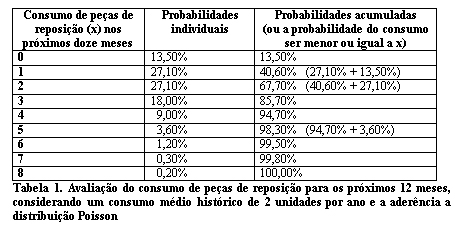 |
| Tabela 1. Avaliação do consumo de peças de reposição para os próximos 12 meses, considerando um consumo médio histórico de 2 unidades por ano e a aderência a distribuição Poisson |
Esta tabela permite chegar as seguintes conclusões para o caso onde o consumo médio histórico é de 2 unidades por ano:
- A probabilidade de não haver solicitações de peças de reposição (x = ZERO) nos próximos 12 meses é de 13,50%. Conseqüentemente, é de 86,50% a probabilidade de haver pelo menos uma solicitação de peças de reposição nos próximos 12 meses. Por outro lado, é nula a probabilidade de haver nove ou mais solicitações por peças de reposição nos próximos doze meses.
- Manter quatro peças de reposição em estoque garante uma probabilidade de não haver falta de 94,70%, ao passo que 5 peças de reposição garantem 98,30% de probabilidade.
- De certa forma, a probabilidade acumulada permite avaliar o nível de serviço, em termos da probabilidade de não haver falta de peças em estoque, para uma determinada quantidade de itens em estoque.
- A soma das probabilidades individuais é igual a 100%. Além disto, a probabilidade de haver pelo menos uma solicitação é igual à diferença entre 100% e a probabilidade de haver zero solicitações por intervalo de tempo.
O conjunto de gráficos a seguir mostra as probabilidades calculadas para diferentes níveis de consumo com base em diferentes valores para o consumo médio histórico (? – lambda). É interessante notar que, na medida que o consumo médio histórico aumenta, o perfil da demanda vai ficando mais simétrico em relação à média. Vale também o raciocínio oposto: menores valores do consumo médio histórico levariam a uma distribuição com perfil mais assimétrico. Este resultado não deixa de ser interessante para representar situações onde um “pico” no consumo causaria mais transtornos que um “vale”, como no caso de algumas peças de reposição de baixo giro.
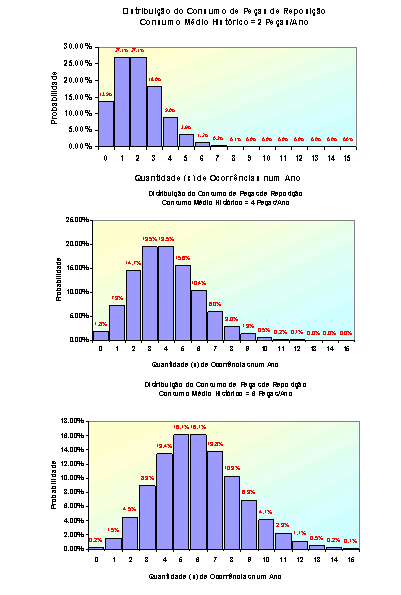 |
| Gráficos. Representação gráfica das probabilidades de ocorrência para diferentes níveis de consumo histórico |
A planilha Microsoft Excel permite implementar facilmente os cálculos relativos às probabilidades individuais e às probabilidades acumuladas. A função POISSON calcula imediatamente, para um determinado consumo de peças de reposição (x) e uma determinada taxa de consumo histórico (?), estas duas probabilidades. Para tanto, devem ser utilizadas as fórmulas a seguir.
= POISSON (x, ? , falso) – probabilidade individual para x
= POISSON (x, ? , verdadeiro) – probabilidade acumulada ate x inclusive
Para que estas fórmulas sejam empregadas corretamente, deve ser observado que tanto as solicitações por peças de reposição (x), quanto a taxa histórica de consumo (?) estejam referenciadas a um mesmo intervalo de tempo.
CONSIDERANDO O TEMPO DE RESPOSTA
Assim como na gestão de estoques de bens de consumo e suas matérias-primas, o nível de estoque de peças de reposição que garante uma determinada probabilidade de não haver falta deve, na realidade, ser determinado para o intervalo de tempo que a empresa esta mais vulnerável, ou seja, o ciclo de ressuprimento. O ciclo de ressuprimento normalmente compreende o intervalo de tempo que vai desde a colocação do pedido junto ao fornecedor ate seu recebimento. É neste período que aumentos imprevistos no consumo de peças de reposição podem levar a falta de estoques.
Um passo básico seria estimar o consumo médio esperado no ciclo de ressuprimento e sua variabilidade, ou seja, o ponto de pedido.Em diversos livros e artigos de logística é possível encontrar a seguinte formula para o ponto de pedido, que é um resultado bastante conhecido entre profissionais e acadêmicos da área:
| |
| onde:D = demanda por unidade de tempo; TR = tempo de resposta do ciclo de ressuprimento, em unidades de tempo k = fator de segurança sD = desvio-padrão da demanda por unidade de tempo |
O que poucos artigos e livros comentam é que este é um resultado aplicável a qualquer distribuição da demanda ou do consumo (Normal, Poisson etc). Desta forma, o ponto de pedido pode ser “reescrito” em termos do consumo médio histórico de peças de reposição por unidade de tempo (D = l) e da variância deste consumo, que no caso da distribuição Poisson é igual ao consumo médio histórico (sD = Öl).
| |
Conforme comentado anteriormente, o ponto de pedido (PP) deve ser determinado em função da probabilidade desejada de não haver falta de estoque durante o tempo de resposta. A função POISSON da planilha Excel pode ser extremamente útil na determinação do ponto de pedido. Através de um procedimento iterativo pode ser avaliado se a probabilidade acumulada do consumo de peças de reposição no tempo de resposta (?*TR) é menor ou maior que a probabilidade de não haver falta de produto em estoque determinada pelo ponto de pedido.
Por exemplo, consideremos que para uma determinada peça de reposição a probabilidade desejada de não haver falta em estoque seja de 90%, o tempo de resposta seja de 2 meses (2/12 avos do ano) e o consumo médio histórico de 4 peças por ano. Testando os valores 1, 2 e 3 como possíveis pontos de pedido na função POISSON do Excel, tem-se:
POISSON(PP,?*TR,verdadeiro)
POISSON(1,4*2/12,verdadeiro)=85,6%- Rejeitar, pois é inferior a probabilidade de 90%
POISSON(2,4*2/12,verdadeiro)=97,0%- Aceitar, pois é superior a probabilidade de 90%
POISSON(3,4*2/12,verdadeiro)=99,5%- Aceitar, pois também é superior a 90%
Neste caso, escolhe-se 2 como ponto de pedido, pois foi o primeiro valor a assegurar a probabilidade de 90% de não haver falta de produto em estoque no tempo de resposta do ciclo de ressuprimento. O ponto de pedido igual a 2 equivale a um fator de segurança (k) igual a 1,625. Este resultado é obtido a partir da última equação. Deve ser observado que se este fator de segurança fosse utilizado numa tabela com os valores para a distribuição Normal acumulada, a probabilidade obtida seria de 94,8%. Isto ilustra que considerar a demanda aderente à distribuição Normal nestas circunstancias poderia trazer informações equivocadas sobre o nível de serviço que está sendo realmente prestado.
CONCLUSÃO
Este artigo complementa a discussão iniciada na edição de Agosto/2002 sobre a gestão de estoques de peças de reposição. No primeiro numero foi identificado um procedimento para lidar com peças de baixíssimo giro (consumo inferior a uma unidade por ano). Este número apresenta os aspectos que devem ser considerados em peças de baixo giro (consumo entre uma e 300 unidades por ano), principalmente com relação à premissa sobre a distribuição do consumo (Normal vs. Poisson). Dependendo da magnitude do consumo e do nível de serviço que deseja prestar, considerar a distribuição Normal pode levar a decisões equivocadas com relação a pontos de pedido e níveis de estoque. Neste sentido, analisar a questão sob a ótica da distribuição Poisson abre caminhos para reduções de estoque, que podem ser consideráveis dependendo da empresa e do setor da economia.
BIBLIOGRAFIA
(1) Maiores informações sobre a distribuição Poisson e outras distribuições podem ser obtidas em websites educacionais e de treinamento. Por exemplo, alguns websites interessantes são:
http://www.math.csusb.edu/faculty/stanton/probstat/poisson.html
http://info.bio.cmu.edu/Courses/03438/PBC97Poisson/PoissonPage.html
http://www.itl.nist.gov/div898/handbook/eda/section3/eda366i.htm
http://hyperphysics.phy-astr.gsu.edu/hbase/math/poifcn.html#c2
http://engineering.uow.edu.au/Courses/Stats/File41.html
(2) Para quem se interessar sobre a discussão do impacto de diferentes distribuições de probabilidade sobre a gestão de estoques, existem diversos artigos neste sentido. Em essência, todos estes artigos procuram responder a seguinte questão: “qual a probabilidade de não haver falta de produto em estoque considerando uma determinada distribuição da demanda no tempo de resposta?” Em alguns casos é possível determinar uma equação que forneça uma solução analítica para tal questão, em outros, são necessários procedimentos mais complexos.
Para um exemplo com distribuição Poisson: VINCENT, P, 1983, “Practical Methods for Accurate Fill Rates”, INFOR, Vol.21, No.2, May, pp.109-120.
Para um exemplo com distribuição Bernoulli: JANSEN, F, HEUTS, R., KOK, T., 1998, “On the (R,s,Q) Inventory Model when Demand is Modeled as a Compound Bernoulli Process”, European Journal of Operational Research, 104, pp. 423-436.
Para exemplos com distribuição Gama: DAS, C., 1976, “Approximate Solution to the (Q,r) Inventory Model for Gamma Lead Time Demand”, Management Science, Vol.22, Issue 9, pp. 1043-1047 e NAMIT, K., CHEN, J., 1999, ”Solutions to the (Q,r) Inventory Model for Gamma Lead Time Demand”, International Journal of Physical Distribution & Logistics Management, Vol.29, No.2, pp. 138-151.
Para exemplos onde é avaliado o impacto de considerar a distribuição Normal em situações onde a demanda não é aderente a esta distribuição: MENTZER, J.T., KRISHNAN, R., 1985, “The Effect of the Assumption of Normality on Inventory Control/Customer Service”, Journal of Business Logistics, Vol. 6, No.1, pp.101-120. e LAU, H., 1989, “Toward an Inventory Control System Under Non-Normal Demand and Lead-Time Uncertainty”, Journal of Business Logistics, Vol.10, No.1, pp. 88-103.