This paper describes a model developed to support investment decisions in a service station network. The model determines the sales potential of service stations in major cities of Brazil like Rio de Janeiro, São Paulo and Recife. It uses explanatory variables like traffic density, number of competitors, average number of pumps per competitor and speed on passing roads. Non linear regression analysis were used to develop the model, with some results here presented.
1. INTRODUÇÃO
Este artigo apresenta um modelo para a avaliação do potencial de vendas em postos de combustíveis urbanos, com vistas à decisão de abertura de uma nova unidade, ao monitoramento do volume de vendas de uma unidade já existente ou à análise de sensibilidade dos fatores que mais influenciam o potencial de vendas num posto. O modelo desenvolvido é uma regressão não-linear múltipla levando em conta variáveis tais como o volume de tráfego, a área da instalação, e o nível de competição nas proximidades do posto.
Para as empresas distribuidoras de combustível que operam no Brasil, a rede de postos de combustível constitui o coração de seu negócio e sua maior fonte de receita. Por outro lado, um posto de combustível é um investimento de centenas de milhares de dólares, englobando não apenas a sua instalação, mas também sua continuidade de operação. Desta forma, o estudo se justifica porque a partir da determinação do potencial de vendas inerente ao local é possível estimar o Retorno Sobre o Investimento (ROI) para uma determinada configuração de funcionamento e grau de concorrência do mercado, de maneira a se avaliar a viabilidade do futuro posto.
Também é possível, para um dado posto existente, confrontar seu potencial de vendas com sua performance atual, utilizando o modelo como instrumento gerencial para controle, melhoria e treinamento de seus operadores. De qualquer forma, a complexidade inerente às decisões de abertura de postos de combustível é um campo fértil para a aplicação de diversas técnicas de modelagem no desenvolvimento de sistemas de apoio à decisão. Além de breve revisão da literatura, nas próximas seções detalharemos as variáveis consideradas, as análises desenvolvidas e os resultados obtidos.
2. REVISÃO DA LITERATURA
São poucos os estudos desta natureza disponíveis na literatura. O trabalho de DIXON (1995) desenvolvido na África do Sul é o que mais se aproxima da linha desenvolvida neste artigo. Seu estudo baseou-se numa amostra de vários postos urbanos localizados na Cidade do Cabo, Durban e Gauteng, sendo o objetivo principal determinar seu potencial de vendas.
Foram inicialmente testadas 100 variáveis explicativas, dentre elas o número de bicos, sinais de trânsito, volume de tráfego, acesso, área e aparência das instalações. Após alguns testes DIXON (1995) chegou a um modelo não-linear composto por 30 variáveis explicativas. O poder de explicação deste modelo pode ser considerado bom, sendo o R2 Ajustado de 80%, 72% e 71% para Durban, Cidade do Cabo e Gauteng respectivamente. O autor evidencia ainda que o uso de termos quadráticos no modelo melhora substancialmente seu poder de explicação. Finalmente, FERNANDES et al. (1997) desenvolveram um modelo para previsão de vendas de combustíveis em postos situados ao longo de rodovias. A fórmula adotada para explicar as vendas agregadas de combustíveis (potencial de mercado) de uma determinada área foi a seguinte:
onde V é o somatório das vendas de todos os postos da área, X1 é o somatório das áreas e X2. é o número de habitantes da área. O poder de explicação deste modelo é elevado, sendo o R2 Ajustado de 94,9% para o potencial da área. Posteriormente os autores utilizaram modelos gravitacionais para fazer análises sobre as vendas individuais de cada posto.
3. CARACTERÍSTICA DA AMOSTRA E VARIÁVEIS CONSIDERADAS
Ao longo de 1996, foram coletados dados de 95 postos de combustíveis nos principais centros urbanos brasileiros como Rio de Janeiro, São Paulo, Belo Horizonte e Recife. A escolha exclusiva de postos urbanos deveu-se ao fato de que, no Brasil, os postos do interior têm seu volume de vendas determinado, sobretudo, pelo grau de empatia e cordialidade no atendimento. Verifica-se que, contrariamente aos postos urbanos, há uma relação de fidelidade entre o posto de combustível e seus clientes nas áreas rurais, sendo também setor de difícil quantificação. A tabela 1 descreve as variáveis explicativas e a variável dependente consideradas no modelo. Já a tabela 2 contém um resumo com as estatísticas descritivas para cada variável.
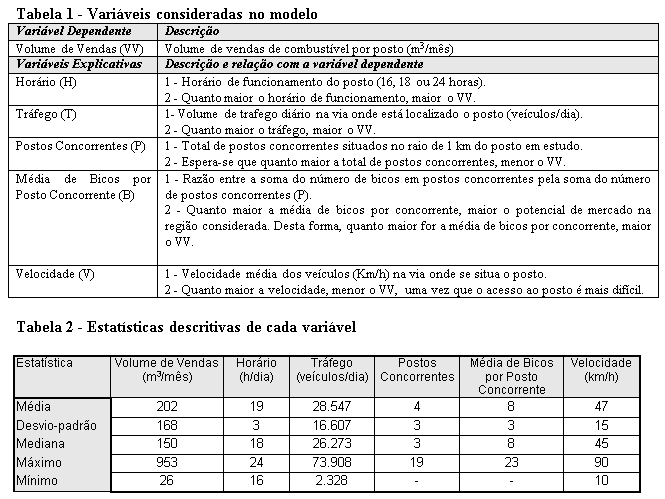 |
A próxima seção descreve a análise inicial realizada com os dados coletados.
4. ANÁLISE PRELIMINAR: REGRESSÃO LINEAR MÚLTIPLA
Definidas as principais variáveis explicativas e o comportamento de seus respectivos sinais, a próxima etapa consistiu na análise residual do seguinte modelo linear múltiplo:
Este modelo apresentou um poder de explicação bastante baixo (R2 Ajustado = 40%) além de apresentar erro padrão bastante elevado, por volta de 131 m3/mês. Entretanto, conforme esperado, as variáveis TRÁFEGO (T), HORÁRIO (H) e MÉDIA DE BICOS POR CONCORRENTE (B) apresentaram contribuições positivas ao Volume de Vendas (VV), enquanto que a soma de postos concorrentes (P) e a velocidade (V) apresentaram contribuições negativas.
Dentre os objetivos da análise residual no modelo linear múltiplo destacamos a exploração da existência ou não de multicolinearidade entre as variáveis explicativas, a identificação de outliers e de observações com elevados coeficientes de alavancagem (h) . Também foram analisadas as distâncias de Cook de cada uma das observações com relação aos demais, bem como avaliou-se a condição de homocedasticidade e normalidade dos resíduos .
Um ponto com elevada alavancagem é uma observação que contém um conjunto incomum de valores para as variáveis explicativas, capaz de exercer forte influência sobre o resultado (coeficientes) da regressão em virtude de seu efeito desproporcional (alavancado), se comparado aos das demais observações.
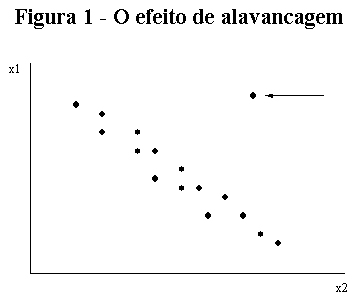 |
Com apenas uma variável explicativa, a determinação de observações incomuns é feita através da análise do histograma da variável explicativa. Quando se trabalha com mais de duas variáveis explicativas, é muito mais complexo determinar graficamente se um ponto é pouco comum. Por exemplo, na figura 1 entre duas variáveis explicativas (x1 e x2), o ponto assinalado no canto superior direito é incomum, afastado da grande nuvem de observações. Todavia, analisando-se os histogramas de x1 e x2 separadamente esta diferença não é percebida. A análise dos coeficientes de alavancagem (h) é uma ferramenta bastante útil para a identificação de observações como a assinalada acima. Altos valores de h indicam que uma observação está exercendo um impacto desproporcional nos coeficientes da regressão. Em geral, podemos considerar pontos de elevada alavancagem , aqueles que satisfazem a relação:
A distância de Cook, por sua vez, é uma estatística utilizada para quantificar o quanto incomum é uma observação, levando em consideração não somente as variáveis explicativas (como é o caso dos coeficientes de alavancagem), mas também seus resíduos. O cálculo do valor crítico para a distância de Cook é dado pela fórmula:
Ao total, foram identificadas 15 observações com elevado coeficiente de alavancagem e elevada distância de Cook, as quais foram removidas da amostra para análise definitiva dos dados, que envolveu o emprego de técnicas de regressão múltipla não-linear.
5. ANÁLISE FINAL: REGRESSÃO MÚLTIPLA NÃO-LINEAR
Dentre os diversos modelos não-lineares testados, o que apresentou melhor capacidade de resposta (medido por um menor erro residual quadrático e por um maior coeficiente R2 Ajustado) foi o seguinte:
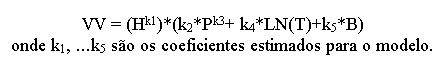 |
Entretanto, a heterocedasticidade verificada nos resíduos levou à divisão da amostra de 80 observações (95 iniciais exclusive as 15 observações com elevados coeficientes de alavancagem e distâncias de Cook) em duas amostras de tamanhos próximos entre si, segundo diferentes critérios testados. Dentre estes, o critério que mais aumentou o poder de explicação do modelo para as duas sub amostras foi a variável velocidade (V). Observações com valores de velocidade maiores que 40 km/h foram agrupados numa amostra (vias de alta velocidade) e observações com valores de velocidade menores ou iguais a 40 km/h (vias de baixa velocidade) foram agrupadas em outra. Devemos lembrar que a mediana da variável velocidade é 40 km/h.
Para a sub amostra com V<=40 km/h, o modelo apresentou um poder de explicação bastante elevado (R2 Ajustado = 80%) além da média dos resíduos ser bastante razoável, por volta de 51 m3/mês. Ainda conforme o esperado, as variáveis TRÁFEGO (T), HORÁRIO (H) e MÉDIA DE BICOS POR CONCORRENTE (B) apresentaram contribuições positivas ao Volume de Vendas (VV), enquanto que a soma de postos concorrentes (P) e a velocidade (V) apresentaram contribuições negativas.
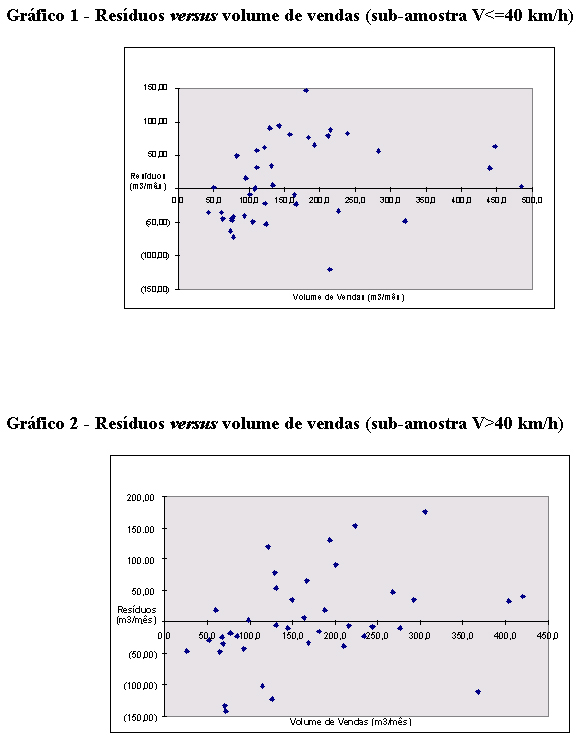
Já para a sub amostra com V>40 km/h, o modelo também apresentou um poder de explicação bastante elevado (R2 Ajustado = 76%) além da média dos resíduos ser bastante razoável, por volta de 52 m3/mês. Ainda conforme o esperado, as variáveis TRÁFEGO (T), HORÁRIO (H) e MÉDIA DE BICOS POR CONCORRENTE (B) apresentaram contribuições positivas ao Volume de Vendas (VV), enquanto que a soma de postos concorrentes (P) e a velocidade (V) apresentaram contribuições negativas. Conforme os gráficos 1 e 2, que nos mostram os resíduos versus o volume de vendas para as duas subamostras, é possível perceber que não se observa qualquer heterocedasticidade.
 |
- CONCLUSÃOO modelo desenvolvido encontra-se atualmente em uso pela empresa distribuidora de combustível proprietária dos 95 postos onde foram coletadas as observações. A facilidade de operação proporcionada pelo emprego de planilhas eletrônicas (por exemplo, a planilha EXCEL ®) permitiu a utilização deste modelo pelo pessoal de campo na decisão de abertura ou não de um novo posto de combustível. Um dos fatores que contribuíram para aceitação do modelo foi o fato de não haver termo constante; assim, quando todas as variáveis explicativas são zero, o volume de vendas (VV) estimado para o posto também é zero.Desenvolvimentos futuros deste modelo estão diretamente relacionados a sua segmentação por centros urbanos, de forma a serem consideradas as características particulares de cada cidade com relação ao perfil de frota, renda média, padrão de tráfego, posturas municipais reguladoras, etc. Há diferenças estruturais claras entre os diversos centros urbanos brasileiros que certamente aumentarão o poder de explicação do modelo no futuro.
8. BIBLIOGRAFIA
DIXON, E.C., 1995; “The Management of a Service Station Network”; Decision Support Services Programs – CSIR Information Services, Pretoria, South Africa.
FERNANDES, C., THEMIDO, I., 1997; “Modelação de Vendas de Combustíveis Líquidos Recorrendo a Modelos Gravitacionais”; Investigação Operacional, v.17, n.1, junho, pp. 41-60.
FREES, E.W., 1996; Data Analysis Using Regression Models – The Business Perspective. 1 ed. New Jersey, Prentice Hall International.