Tendo em vista a crescente importância das atividades logísticas no Brasil, torna-se cada vez mais necessário mensurar seus diferentes componentes. Especificamente, os transportes representam, em média, 64% do custo logístico das empresas, constituindo um objeto de análise importante para acadêmicos e gestores. Com base nessa perspectiva, é apresentado um estudo de caso que busca analisar o comportamento do preço de frete no setor de agronegócios, um dos mais dinâmicos da economia brasileira.
- INTRODUÇÃO
O agronegócio representa quase 33% do PIB nacional e envolve em torno de 37% da População Economicamente Ativa (PEA). Este setor responde ainda por 42% das exportações brasileiras e coloca o País em uma posição de destaque no cenário internacional. (MAPA, 2004).
Entretanto, o agronegócio enfrenta algumas dificuldades, principalmente em infraestrutura – o que pode provocar questionamentos quanto à capacidade de manutenção dessa posição de destaque. Segundo Rodrigues (2004, citado por Carvalho e Caixeta Filho, 2007), a falta de infraestrutura pode resultar em retenção da produção no campo, uma vez que os produtores rurais podem ficar sem meios para comercializar ou estocar seus produtos, o que caracterizaria a chamada “perspectiva da crise de abundância”. Para Castro (1995, citado por Carvalho e Caixeta Filho (2007), a logística eficiente é condição básica para a competitividade de todos os setores da economia.
Buscando uma análise mais profunda sobre o mercado de frete, as previsões do preço são conduzidas por meio de cinco diferentes métodos, os quais têm sido usados nas mais diversas aplicações, desde previsão de indicadores financeiros e otimização de funções até aplicações ligadas à medicina. Seus resultados são analisados à luz da combinação e da competição, duas abordagens alternativas para lidar com previsões geradas por diversos métodos.
Devido à extensão do assunto, o presente artigo será dividido em duas partes. Na primeira, serão abordadas as vantagens da previsão combinada na obtenção de um resultado mais preciso, além da análise de três dos cinco principais métodos de previsão usados atualmente pelas empresas (Modelo Econométrico, Decomposição Clássica e ARIMA). Os dois últimos métodos (Redes Neurais e Algoritmos Genéticos) serão analisados na segunda parte, que terá ainda um estudo de caso, que vai abordar a previsão dos preços de frete para uma empresa do setor de Agronegócios.
- COMBINAÇÃO X COMPETIÇÃO DE PREVISÕES
A combinação de previsões tem sido estudada há muito tempo. Evidências empíricas apontam que as previsões melhoram quando previsões individuais são combinadas. Gordon (1924, citado por Chase Jr, 2000), um dos primeiros a conduzir pesquisas nesse campo, fornece um bom exemplo, quando mostra uma das formas mais comuns de combinação de previsões – em eventos esportivos, como o boxe. Em busca do resultado mais justo, é feita uma média das notas dos três juízes.
As vantagens da previsão combinada se tornam mais evidentes em casos de alta incerteza ou quando as previsões são negativamente correlacionadas. Para Chase Jr (2000) a ideia de combinar previsões é melhor na medida em que os vieses dos métodos e/ou daqueles que fazem as previsões serão compensados de um para outro. Além disso, as previsões são geradas por indivíduos com dados e objetivos diferentes dentro das empresas. Combiná-las torna-se favorável, na medida em que deixa a previsão final mais equilibrada.
Existem diversos métodos para combinar previsões, sendo os mais básicos os que fornecem os melhores resultados: a média simples e a média ponderada. Por exemplo, a notação para média simples de três métodos de previsão é:
 |
Elaborar uma previsão combinada requer a escolha de pesos para cada método. Essa decisão pode ser feita através softwares de otimização, cujo objetivo é determinar os pesos que minimizem o erro de previsão. A soma dos pesos é restrita a um. A notação para a média ponderada é apresentada a seguir:
Por outro lado, a competição consiste no confronto entre diferentes previsões individuais e na escolha da melhor delas. É uma abordagem interessante, considerando que determinado método pode apresentar maior acurácia para um conjunto de dados. Nesse caso, erros muito elevados em outras previsões não são incorporados na melhor delas.
Não existe uma abordagem de previsão que seja comprovadamente a melhor. Os tipos de dados e os objetivos a serem alcançados devem ser analisados e cada caso avaliado individualmente. As previsões combinadas, além das evidências empíricas que comprovam sua maior eficácia, são benéficas ao gerar um resultado mais equilibrado, mais próximo da real tendência central ao longo do tempo. Não obstante, a competição de previsões, pode gerar um resultado mais preciso. Sobretudo quando as previsões são positivamente correlacionadas. Flores e White (1989) consideram que a melhor abordagem a ser usada é aquela que gera sistematicamente os melhores resultados ao longo do tempo, seja a combinação ou a competição.
3. PRINCIPAIS MÉTODOS DE PREVISÃO
Na primeira parte desse artigo, abordaremos três dos cinco principais métodos de previsão – passíveis de combinação e competição – adotados pelas empresas.
3.1 MODELO ECONOMÉTRICO
A econometria é a ciência que une a economia, a estatística e a matemática. Para Gujarati (2000, citado por Rangel, 2007), o método da pesquisa econométrica visa, essencialmente, a uma conjunção da teoria econômica com medidas concretas, usando como ponte a teoria e as técnicas de inferência estatística.
Análise de regressão é uma das técnicas estatísticas usadas na econometria para explicar uma variável dependente Y por meio de uma ou mais variáveis independentes Xi. A correlação entre as variáveis independentes na regressão múltipla não pode ser alta. Quando isso ocorre, a contribuição das variáveis para o modelo é a similar, o que não gera previsões mais precisas, visto que não há informações realmente “novas” para explicar o comportamento da variável dependente.
A equação que descreve um modelo de regressão múltipla é dada pela função linear:
 |
Os parâmetros do modelo são estimados através do método dos mínimos quadrados, a partir do conjunto de dados, por softwares como o Excel e o SPSS. Hanke e Wichern (2005) descrevem o significado dos coeficientes de regressão:
“O coeficiente parcial da regressão mede a variação média na variável dependente por unidade de variação na variável independente, mantendo as demais variáveis independentes constantes.”
Por exemplo, Castro (2003) estuda a formação dos preços no transporte de carga no Brasil. Para explicar o preço do frete (variável dependente), o autor usa como variáveis explicativas: preço do combustível, salário médio, despesa com seguro por tonelada, distância média de transporte, carregamento médio dos veículos, tamanho médio dos lotes e porcentagem das receitas em carga fracionada.
Conforme visto, os modelos econométricos podem ter diversas aplicações. É importante ressaltar que o acréscimo de variáveis a um modelo não o torna, necessariamente, mais preciso, principalmente quando o índice de correlação entre as mesmas for elevado. Por isso, é fundamental analisar a real contribuição de uma variável a um modelo. A ocorrência de multicolinearidade eleva o erro padrão dos coeficientes de regressão, tornando a variável menos significativa. Ou seja, no limite, esses coeficientes podem assumir qualquer valor, inclusive zero, o que pode prejudicar as análises do tomador de decisão.
3.2 DECOMPOSIÇÃO CLÁSSICA
O método de decomposição clássica é um dos métodos mais simples e de fácil aplicação usado para gerar previsões a partir de séries temporais. Morretin e Toloi (1987, citados por Werner e Ribeiro, 2003) definem uma série temporal como qualquer conjunto de observações ordenadas no tempo. Hanke e Wichern (2005) apresentam a seguinte definição:
“Uma série temporal consiste em dados coletados, registrados ou observados ao longo de sucessivos incrementos de tempo”
Os registros de uma série temporal devem ser feitos a intervalos fixos de tempo. Em geral, são feitos anualmente ou mensalmente, dependendo do objetivo da previsão. Para gerar uma boa previsão, a amostra deve ser considerável. Tabachnick e Fidell (2001) consideram que o mínimo deve ser de 50 observações. Normalmente, os valores de uma série são autocorrelacionados, ou seja, a variação de um valor impacta os vizinhos. Essa dependência produz um padrão de variabilidade que pode ser usado para prever valores futuros e ajudar na gestão de operações comerciais (Hanke e Wichern, 2005).
Uma série temporal é composta por quatro elementos básicos:
- Tendência (T): É a componente que mostra o crescimento ou declínio da série ao longo do tempo.
- Ciclo (C): A componente cíclica representa o movimento ondulatório ou ciclo de uma série com um ou mais anos de duração, que tende a ser periódico ao longo de vários anos.
- Sazonalidade (S): É a flutuação ondulatória da série dentro de um ano. Sofre influência do clima e de eventos como natal, férias escolares e feriados.
- Irregular (I): É a componente que representa as flutuações aleatórias da série, que não podem ser previstas. Também pode ser chamada de ruído aleatório ou erro.
A Figura 1 ilustra uma série com sazonalidade e pequena tendência de crescimento.
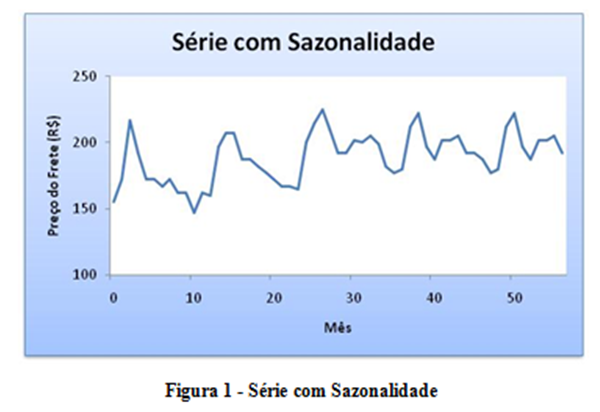 |
A decomposição clássica pode gerar previsões (Y) através de dois modelos, o aditivo e o multiplicativo. As equações são apresentadas a seguir:
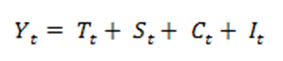 |
e | 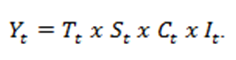 |
Considerando a dificuldade em trabalhar com ciclos – podem ser confundidos com a tendência (T) – alguns autores simplificam os modelos de previsão:
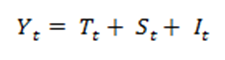 |
e | 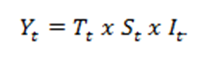 |
Outros ainda propõem simplificações diferentes, levando em conta que o erro aleatório não pode ser calculado:
| e |
O cálculo dos índices é muito simples – pode ser feito em Excel – constituindo uma das grandes vantagens desse método. Além disso, embora a amostra deva ter tamanho considerável, é feita para apenas uma variável, diferente do modelo econométrico, quando, em geral, mais de duas variáveis são necessárias. Em contrapartida, na decomposição clássica, não são analisados fatores externos à série temporal.
3.2 ARIMA
Os modelos ARIMA (Auto-Regressive Integrated Moving-Average ou Auto-Regressivos Integrados às Médias Móveis), assim como no método de decomposição clássica, são utilizados para previsão de séries temporais. São modelos lineares capazes de representar tanto séries estacionárias, quanto não-estacionárias (Hanke e Wichern, 2005). Também recebem o nome de modelos Box-Jenkins, autores que desenvolveram a metodologia na década de 70.
Segundo Werner e Ribeiro (2003), os modelos Box-Jenkins partem da idéia de que cada valor da série (temporal) pode ser explicado por valores prévios, a partir do uso da estrutura de correlação temporal. Esta também pode ser denominada autocorrelação. Cabe destacar a diferença entre a autocorrelação nas séries temporais e a correlação entre as variáveis no modelo econométrico. No primeiro caso, é a relação entre os próprios valores da série que gera uma estrutura capaz de realizar previsões. Ou seja, é fundamental que esta seja forte. No segundo, analisa-se a relação entre diferentes variáveis explicativas e a variável independente. Neste caso, é importante que as variáveis explicativas não sejam correlacionadas entre si para um bom desempenho do modelo.
O modelo é composto por três termos – o auto-regressivo, termo de tendência ou filtro de integração e o das médias móveis – representados pelas letras p, d e q respectivamente. Esses termos podem ser combinados, gerando diferentes modelos: estacionários (ARMA), não–estacionários (ARIMA) e sazonais (SARIMA).
Tabachnick e Fidell (2001) apresentam a seguinte definição para os componentes p, d e q:
- Termo auto-regressivo (p) – Número de termos do modelo que descreve a dependência entre observações sucessivas.
- Termo de médias móveis (q) – É o número de termos que descreve a persistência de um choque aleatório de uma observação para outra.
- Termo de tendência (d) – Termos necessários para transformar uma série não-estacionária em estacionária.
As previsões ARIMA são realizadas seguindo as etapas do fluxograma da Figura 2. Caso o modelo sugerido não seja adequado, o procedimento é repetido.
 |
Os modelos estacionários, embora não sejam muito comuns, podem ser apenas modelos auto-regressivos (AR) ou modelos de médias móveis (MA). A seguir são apresentadas funções que descrevem esses modelos, além do modelo auto-regressivo de médias móveis (ARMA):
Modelo Auto Regressivo:
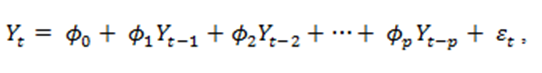 |
 |
Caso a série analisada seja não-estacionária, ou seja, com tendência e sazonalidade, é preciso transformá-la em uma série estacionária, tomando sucessivas diferenças. A primeira diferença de uma série Yt é dada por:
Um modelo ARIMA com p =1 e q=1 é dado por:
Nos modelos SARIMA, muito usados quando a série é impactada pelo clima ou determinados eventos anuais, além dos componentes p, d e q não sazonais, são acrescentados parâmetros sazonais P, D e Q.
A utilização da metodologia Box-Jenkins requer conhecimento e atenção do previsor. A escolha de um modelo adequado é fundamental para realização de uma boa previsão. Essa escolha é baseada em alguns testes estatísticos, que não fazem parte do escopo do presente trabalho. A complexidade dos algoritmos usados para definição dos coeficientes do modelo torna fundamental o uso de softwares especializados, como o SPSS.
4 Conclusão
A logística cresce em importância dentro das empresas brasileiras e, junto com ela, se desenvolve também a preocupação em relação aos seus gastos. Por isso, é importante que se saiba mensurar seus diferentes componentes, principalmente o custo de transporte, que representa 64% dos gastos do agronegócio com logística.
Entretanto, encontrar modelos que se adequem ao conjunto de dados e aos objetivos das empresas é uma tarefa delicada e que requer conhecimento analítico. Na segunda parte desse artigo serão estudados os dois últimos métodos de previsão (Redes Neurais e Algoritmos Genéticos) – passíveis de combinação e competição – adotados pelas empresas, além da apresentação de um estudo de caso, que vai abordar a previsão dos preços de frete para uma empresa do setor de Agronegócios.
5 Bibliografia
CARVALHO, L. B.; CAIXETA FILHO, J. V. Comportamento do Mercado de Preços de Fretes Rodoviários de Açúcar para Exportação no Estado de São Paulo, Revista de Economia e Agronegócio, v. 5, n. 1, 2007.
CASTRO, N. Formação de Preços no Transporte de Carga, Pesquisa e Planejamento Econômico, v. 33, n. 1, 2003. Disponível em http://ppe.ipea.gov.br/index.php/ppe/article/viewFile/89/64. Acesso em 25/03/2010.
CHASE JR, W. C. Composite Forecasting: Combining Forecasts for Improved Accuracy, The Journal of Business Forecasting Methods & Systems. p 2, 20-22, 2000.
FAUSETT, L. Fundamentals of Neural Networks, Upper Saddle River: Prentice Hall, 1994. 461 p.
FLORES, B. E.; WHITE, E. M. Combining Forecasts: Why, When and How, The Journal of Business Forecasting Methods & Systems. p 2-5, 1989.
GURNEY, K. An Introduction to Neural Networks. London: CRC Press, 2003. 234 p.
HANKE, J. E., WICHERN, D. W. Business Forecasting. 8. ed. New Jersey: Pearson Prentice Hall, 2005. 535p.
MAPA – Ministério da Agricultura, Pecuária e Abastecimento. Disponível em http://www.agricultura.gov.br/. Acesso em 30/03/2010.
MOREIRA, L. M.. Multicolinearidade em Análise de Regressão. 2003. Disponível em: http://www.ead.fea.usp.br/Semead/9semead/resultado_semead/trabalhosPDF/455.pdf. Acesso em 10/03/2010.
NEVES, M. V. Utilização de Redes Neurais para Predição de Series Temporais Aplicada a Detecção de Ociosidade Computacional
PACHECO, M. A. C. Algoritmos Genéticos: Princípios e Aplicações. 1999. Disponível em http://www.ica.ele.puc-rio.br/Downloads%5C38/CE-Apostila-Comp-Evol.pdf. Acesso em 15/03/2010.
RANGEL, L. A. A Utilização da Econometria na Pesquisa Empírica da Contabilidade, Revista CRCRS. 2007 Disponível em: http://www.crcrs.org.br/revistaeletronica/artigos/05_leandro.pdf. Acesso em 04/03/2010.
SANTA ROSA, H. N. Redes Neurais na previsão de Séries Temporais. 2004. Disponível em: http://inf.unisul.br/~ines/workcomp/cd/pdfs/2878.pdf. Acesso em 08/03/2010.
SOARES, G. L. Algoritmos Genéticos: Estudos, Novas Técnicas e Aplicações. 1997. 137 f . Dissertação (Mestrado em Engenharia Elétrica) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte. 1997.
TABACHNICK, B. G.; FIDELL, L. S. Using Multivariate Statistics. 4. ed. Needham Heights,: Allyn & Bacon, 2001. 966 p.
WERNER, L.; RIBEIRO, J. L. D., Previsão de Demanda: Uma Aplicação dos Modelos Box-Jenkins na Área de Assistência Técnica de Computadores Pessoais. Gestão e Produção, v.10, n.1, p 47-67, 2003.
